��Ŀ����
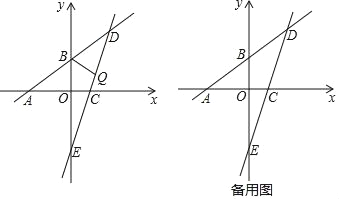
����Ŀ����֪����ͼ��һ�κ���![]() ��ͼ��ֱ���x�ᡢy���ཻ�ڵ�A��B�����뾭����C��2��0����һ�κ���y=kx+b��ͼ���ཻ�ڵ�D����D�ĺ�����Ϊ4��ֱ��CD��y���ཻ�ڵ�E��
��ͼ��ֱ���x�ᡢy���ཻ�ڵ�A��B�����뾭����C��2��0����һ�κ���y=kx+b��ͼ���ཻ�ڵ�D����D�ĺ�����Ϊ4��ֱ��CD��y���ཻ�ڵ�E��
��1��ֱ��CD�ĺ�������ʽΪ�� ������ֱ��д�������
��2����QΪ�߶�DE�ϵ�һ�����㣬����BQ��
����ֱ��BQ����BDE�������Ϊ1��2�����֣������Q�����ꣻ
������BQD����ֱ��BQ���ۣ�ʹ�õ�Dǡ������ֱ��AB�·�����������,��ֱ��д����Q������: .
���𰸡���1��y=3x��6����2������![]() ����2����
����2����![]() ��2�����ڴ��ڣ���Q������Ϊ��3��3����
��2�����ڴ��ڣ���Q������Ϊ��3��3����![]() ��
��![]() ����
����
��������
��1�����C��D�������꼴�ɽ�����⣻
��2��������������S��BEQ=![]() S��BDE��S��BEQ=
S��BDE��S��BEQ=![]() S��BDE�ֱ����̼��ɣ�
S��BDE�ֱ����̼��ɣ�
������������������D����x�������ϣ���Ϊ��D1��ʱ����ͼ2��������D����y�������ϣ���Ϊ��D2��ʱ����ͼ3�����ֱ���⼴��.
�⣺��1�������⣺D��4��6����C��2��0����
��ֱ��CD�Ľ���ʽΪy=kx+b��
����![]() ��
��
���![]() ��
��
��ֱ��CD�Ľ���ʽΪy=3x��6��
�ʴ�Ϊ��y=3x��6��
��2���١�ֱ��BQ����BDE�������Ϊ1��2�����֣�
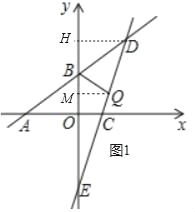
��S��BEQ=![]() S��BDE��S��BEQ=
S��BDE��S��BEQ=![]() S��BDE��
S��BDE��
��y=![]() x+3�У���x=0ʱ��y=3����x=4ʱ��y=6��
x+3�У���x=0ʱ��y=3����x=4ʱ��y=6��
��B��0��3����D��4��6����
��y=3x��6�У���x=0ʱ��y=��6��
��E��0����6����
��BE=9��
��ͼ1�У�����D��DH��y���ڵ�H����DH=4��
��S��BDE=![]() BEDH=
BEDH=![]() ��9��4=18��
��9��4=18��
��S��BEQ=![]() ��18=6��S��BEQ=
��18=6��S��BEQ=![]() ��18=12��
��18=12��
��Q��t��3t��6����������֪t��0��
����Q��QM��y���ڵ�M����QM=t��
��![]() ��9��t=12��
��9��t=12��
���t=![]() ��
��![]() ��
��
��t=![]() ʱ��3t��6=��2��
ʱ��3t��6=��2��
��t=![]() ʱ3t��6=2��
ʱ3t��6=2��
��Q��������![]() ����2����
����2����![]() ��2����
��2����
������D����x�������ϣ���Ϊ��D1��ʱ����ͼ2����
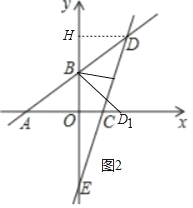
�ɣ�2��֪B��0��3����D��4��6����
��BH=BO=3��
�ɷ��۵�BD=BD1��
����Rt��DHB��Rt��D1OB��
![]() ��
��
��Rt��DHB��Rt��D1OB��HL����
���DBH=��D1BO��
�ɷ��۵���DBQ=��D1BQ��
���HBQ=��OBQ=90�㣬
��BQ��x����
����Q��������Ϊ3��
��y=3x��6�У���y=3ʱ��x=3��
��Q��3��3����
����D����y�������ϣ���Ϊ��D2��ʱ����ͼ3����
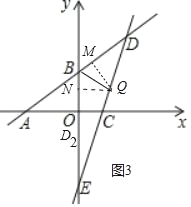
����Q��QM��BD��QN��OB������ֱ�Ϊ��M��N��
�ɷ��۵���DBQ=��D2BQ��
��QM=QN��
�ɣ�2��֪S��BDE=18����S��BQD+S��BQE=18��
��![]() BDQM+
BDQM+![]() BEQN=18��
BEQN=18��
������֮��ľ��빫ʽ����BD=![]() =5��
=5��
��![]() ��5QN+
��5QN+![]() ��9QN=18��
��9QN=18��
���QN=![]() ��
��
����Q�ĺ�����Ϊ![]() ��
��
��y=3x��6�У���x=![]() ʱ��y=
ʱ��y=![]() ��
��
��Q��![]() ��
��![]() ����
����
�ۺ�֪����Q������Ϊ��3��3����![]() ��
��![]() ����
����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�