题目内容
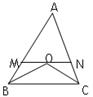
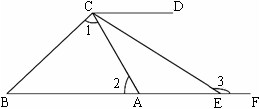
如图,E是边长为1的正方形ABCD的对角线BD上一点,且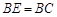 ,P为CE上任意一点,
,P为CE上任意一点,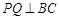 于点Q,
于点Q,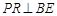 于点R,则
于点R,则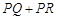 的值是( )
的值是( )
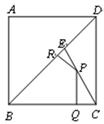
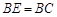 ,P为CE上任意一点,
,P为CE上任意一点,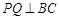 于点Q,
于点Q,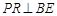 于点R,则
于点R,则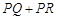 的值是( )
的值是( )
A.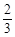 | B.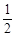 | C.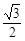 | D.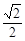 |
D
试题分析:连接BP,过E作EF⊥BC于F,由S△BPC+S△BPE=S△BEC根据三角形的面积公式可得
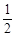 BC•PQ+
BC•PQ+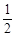 BE•PR=
BE•PR=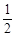 BC•EF,由BE=BC=1可得PQ+PR=EF,根据正方形的性质可得∠DBC=45°,在Rt△BEF中,∠EBF=45°,BE=1,sin45°=
BC•EF,由BE=BC=1可得PQ+PR=EF,根据正方形的性质可得∠DBC=45°,在Rt△BEF中,∠EBF=45°,BE=1,sin45°= ,即可求得EF的长,从而可以求得结果.
,即可求得EF的长,从而可以求得结果.解:连接BP,过E作EF⊥BC于F

∵S△BPC+S△BPE=S△BEC
∴
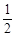 BC•PQ+
BC•PQ+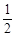 BE•PR=
BE•PR=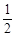 BC•EF,
BC•EF,∵BE=BC=1,
∴PQ+PR=EF,
∵四边形ABCD是正方形,
∴∠DBC=45°,
∵在Rt△BEF中,∠EBF=45°,BE=1,sin45°=
 ,
,∴

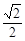 ,
,∴EF=
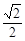 ,即PQ+PR=
,即PQ+PR=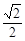 .
.∴PQ+PR的值为
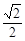 .
.故选D.
点评:解答本题的难点是证明底边上任意一点到等腰三角形两腰的距离等于一腰上的高.在突破难点时,要充分利用正方形的性质和三角形面积公式.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
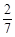 ,求这个正多边形的边数和它一个内角的度数。
,求这个正多边形的边数和它一个内角的度数。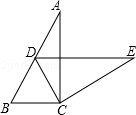
 ,BC=3,△DEF是边长为a(a为小于3的常数)的等边三角形,将△DEF沿AC方向平移,使点D在线段AC上,DE∥AB,设△DEF与△ABC重叠部分的周长为T。
,BC=3,△DEF是边长为a(a为小于3的常数)的等边三角形,将△DEF沿AC方向平移,使点D在线段AC上,DE∥AB,设△DEF与△ABC重叠部分的周长为T。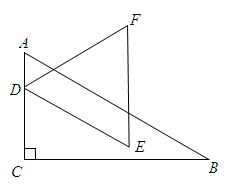
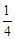 ,当a=2时,求T的值;
,当a=2时,求T的值;