题目内容
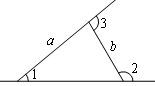
如图,在Rt△ABC中,∠ACB=90°,∠A=α,将△ABC绕点C按顺时针方向旋转后得到△EDC,此时点D在AB边上,则旋转角的大小为 .
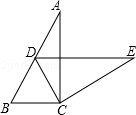

2α
分析:由在Rt△ABC中,∠ACB=90°,∠A=α,可求得:∠B=90°﹣α,由旋转的性质可得:CB=CD,根据等边对等角的性质可得∠CDB=∠B=90°﹣α,然后由三角形内角和定理,求得答案:
∵在Rt△ABC中,∠ACB=90°,∠A=α,∴∠B=90°﹣α。
由旋转的性质可得:CB=CD,∴∠CDB=∠B=90°﹣α。
∴∠BCD=180°﹣∠B﹣∠CDB=2α,即旋转角的大小为2α。

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 ,求AD的长.
,求AD的长.
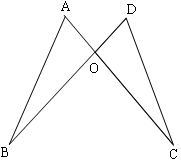
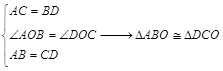
 中,
中,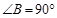 ,若按图中虚线剪去
,若按图中虚线剪去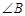 ,则
,则 等于( )
等于( )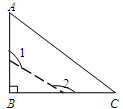
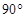
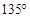
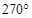
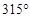
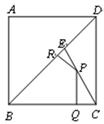
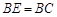 ,P为CE上任意一点,
,P为CE上任意一点,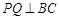 于点Q,
于点Q,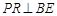 于点R,则
于点R,则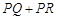 的值是( )
的值是( )