题目内容
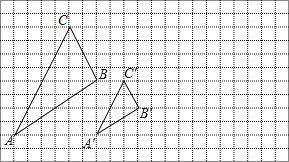
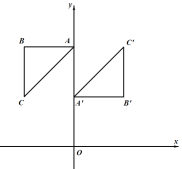
【题目】如图,在Rt△ABC中,∠B=90°,AB=BC,A、B的坐标分别为(0,4),(-2,4),将△ABC绕点P旋转180°后得到△A′B′C′,其中点B的对应点B′的坐标为(2,2).
(1)求出点C的坐标;
(2)求点P的坐标,并求出点C的对应点C′的坐标.

【答案】(1)C(-2,2);(2)P(0,3),C′(2,4).
【解析】
(1)由已知得△ABC是等腰直角三角形,由A、B两点的坐标可知: AB // x轴,可得C的坐标;
(2)先由旋转得:△ABC是等腰直角三角形,且边长为2,根据B的坐标为(2,2),),可知C的坐标;由A和A的坐标可得P的坐标.
解:(1)∵A、B的坐标分别为(0,4),(-2,4),∴AB∥x轴,AB=2
∵∠B=90°, ∴C(-2,2);
(2)由旋转得:AB=BC=2, ∵点B的对应点B的坐标为(2,2) ∴C(2,4)
由A(0,4)得:A(0,2),∴P(0,3)

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目