题目内容
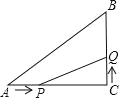
【题目】如图，在△ABC中，∠C=90°，AC=6cm，BC=8cm，点P从A点开始沿AC边向点C以1m/s的速度运动，在C点停止，点Q从C点开始沿CB方向向点B以2m/s的速度移动，在点B停止．
（1）如果点P、Q分别从A、C同时出发，经几秒钟，使S△QPC=8cm2；
（2）如果P从点A先出发2s，点Q再从C点出发，经过几秒后S△QPC=4cm2．
【答案】(1)、2秒；(2)、4秒.
【解析】
试题分析：本题可设P出发xs后，S△QPC符合已知条件：在(1)中，AP=xm，PC=（6﹣x）m，QC=2xm；在(2)中，AP=xm，PC=（6﹣x）m，QC=2（x﹣2）m，进而可列出方程，求出答案．
试题解析：(1)、P、Q同时出发，设xs时，S△QPC=8cm2，由题意得： 
（6﹣x）2x=8， ∴x2﹣6x+8=0，解得：x1=2，x2=4． 经2秒点P到离A点1×2=2cm处，点Q离C点2×2=4cm处，经4s点P到离A点1×4=4cm处，点Q点C点2×4=8cm处，经验证，它们都符合要求．
(2)、设P出发ts时S△QPC=4cm2，则Q运动的时间为（t﹣2）秒，由题意得： 
（6﹣t）2（t﹣2）=4，∴t2﹣8t+16=0， 解得：t1=t2=4
因此经4秒点P离A点1×4=4cm，点Q离C点2×（4﹣2）=4cm，符合题意．
练习册系列答案
相关题目
