题目内容
【题目】在矩形ABCD中,AB=6,BC=8,点E为BC延长线上一点,且BD=BE,连接DE,Q为DE的中点,有一动点P从B点出发,沿BC以每秒1个单位的速度向E点运动,运动时间为t秒.
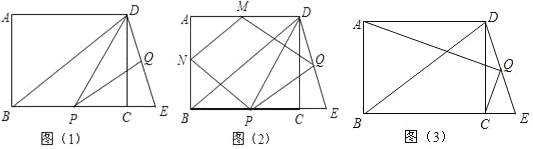
(1)如图1,连接DP、PQ,则S△DPQ=_____(用含t的式子表示);
(2)如图2,M、N分别为AB、AD的中点,当t为何值时,四边形MNQP为平行四边形?请说明理由;
(3)如图3,连接CQ,AQ,试判断AQ、CQ的位置关系并加以证明.
【答案】(1)15﹣![]() t;(2)t=5时,四边形MNQP为平行四边形;(3)AQ⊥CQ.
t;(2)t=5时,四边形MNQP为平行四边形;(3)AQ⊥CQ.
【解析】
(1)由勾股定理可求BD=10,由三角形的面积公式和S△DPQ=![]() (S△BED﹣S△BDP)可求解;
(S△BED﹣S△BDP)可求解;
(2)当t=5时,可得BP=5=![]() BE,由中位线定理可得MN∥BD,MN=
BE,由中位线定理可得MN∥BD,MN=![]() BD=5,PQ∥BD,PQ=
BD=5,PQ∥BD,PQ=![]() BD=5,可得MN∥PQ,MN=PQ,可得结论.
BD=5,可得MN∥PQ,MN=PQ,可得结论.
(3)连接BQ,由等腰三角形的性质可得∠AQD+∠BQA=90°,由直角三角形的性质可得DQ=CQ,∠DCQ=∠CDQ,由“SAS”可证△ADQ≌△BCQ,可得∠AQD=∠BQC,即可得结论.
解:(1)∵四边形ABCD是矩形,AB=6,BC=8,
∴BC=8,CD=6,
∴BD=![]() =10
=10
∴BD=BE=10
∵Q为DE的中点,
∴S△DPQ=![]() S△DPE,
S△DPE,
∴S△DPQ=![]() (S△BED﹣S△BDP)=
(S△BED﹣S△BDP)=![]() ,
,
故答案为15﹣![]() t
t
(2)当t=5时,四边形MNQP为平行四边形,
理由如下:∵M、N分别为AB、AD的中点,
∴MN∥BD,MN=![]() BD=5,
BD=5,
∵t=5时,
∴BP=5=![]() BE,且点Q是DE的中点,
BE,且点Q是DE的中点,
∴PQ∥BD,PQ=BD=5
∴MN∥PQ,MN=PQ
∴四边形MNQP是平行四边形
(3)AQ⊥CQ
理由如下:如图,连接BQ,
∵BD=BE,点Q是DE中点,
∴BQ⊥DE,
∴∠AQD+∠BQA=90°
∵在Rt△DCE中,点Q是DE中点,
∴DQ=CQ,
∴∠DCQ=∠CDQ,且∠ADC=∠BCD=90°
∴∠ADQ=∠BCQ,且BC=AD,DQ=CQ
∴△ADQ≌△BCQ(SAS)
∴∠AQD=∠BQC,且∴∠AQD+∠BQA=90°
∴∠BQC+∠BQA=90°
∴∠AQC=90°
∴AQ⊥CQ

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案