题目内容
【题目】以边长为![]() 的正方形的中心
的正方形的中心![]() 为端点,引两条相互垂直的射线,分别与正方形的边交于
为端点,引两条相互垂直的射线,分别与正方形的边交于![]() 、
、![]() 两点,则线段
两点,则线段![]() 的取值范围是________.
的取值范围是________.
【答案】![]()
【解析】
先证明△AOE≌△DOF,进而得到OE=OF,此为解决该题的关键性结论;求出OE的范围,借助勾股定理即可解决问题.
如图所示:
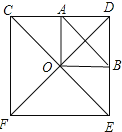
∵四边形CDEF是正方形,
∴∠OCD=∠ODB=45°,∠COD=90°,OC=OD,
∵AO⊥OB,
∴∠AOB=90°,
∴∠COA+∠AOD=90°,∠AOD+∠DOB=90°,
∴∠COA=∠DOB,
在△COA和△DOB中,
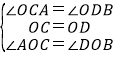 ,
,
∴△COA≌△DOB(ASA),
∴OA=OB,
设OA=OB=a,
∵∠AOB=90°,
∴△AOB是等腰直角三角形,
由勾股定理得:AB2=OA2+OB2=2a2,
由题意可得:1≤a≤![]() ,
,
∴![]() .
.
故答案是:![]() .
.

练习册系列答案
相关题目