题目内容
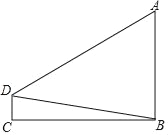
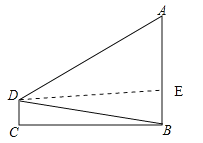
【题目】如图，两座建筑物的水平距离BC为40m，从D点测得A点的仰角为30°，B点的俯角为10°，求建筑物AB的高度（结果保留小数点后一位）．
参考数据sin10°≈0.17，cos10°≈0.98，tan10°≈0.18，
取1.732．
【答案】30.3m.
【解析】分析：过点D作DE⊥AB，利用解直角三角形的计算解答即可．
详解：如图，根据题意，BC=40，∠DCB=90°，∠ABC=90°．
过点D作DE⊥AB，垂足为E，则∠DEB=90°，∠ADE=30°，∠BDE=10°，可得四边形DCBE为矩形，∴DE=BC=40．
在Rt△ADE中，tan∠ADE=
，
∴AE=DEtan30°=
．
在Rt△DEB中，tan∠BDE=
，
∴BE=DEtan10°=40×0.18=7.2，
∴AB=AE+BE=23.09+7.2=30.29≈30.3．
答：建筑物AB的高度约为30.3m．
练习册系列答案
相关题目
