题目内容
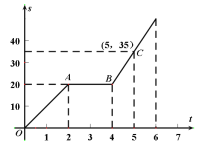
【题目】小明骑自行车从甲地到乙地,图中的折线表示小明行驶的路程![]() 与所用时间
与所用时间![]() 之间的函数关系.试根据函数图像解答下列问题:
之间的函数关系.试根据函数图像解答下列问题:
(1)小明在途中停留了____![]() ,小明在停留之前的速度为____
,小明在停留之前的速度为____![]() ;
;
(2)求线段![]() 的函数表达式;
的函数表达式;
(3)小明出发1小时后,小华也从甲地沿相同路径匀速向乙地骑行,![]()
![]() 时,两人同时到达乙地,求
时,两人同时到达乙地,求![]() 为何值时,两人在途中相遇.
为何值时,两人在途中相遇.
【答案】2; 10;
(2)s=15t-40![]() ;
;
(3)t=3h或t=6h.
【解析】
(1)由图象中的信息可知:小明从第2小时到第4小时行驶的路程没有发生变化,所以途中停留了2![]() ;小明2小时内行驶的路程是20 km,据此可以求出他的速度;
;小明2小时内行驶的路程是20 km,据此可以求出他的速度;
(2)由图象可知:B(4,20),C(5,35),设线段![]() 的函数表达式为s=kt+b,代入后得到方程组,解方程组即可;
的函数表达式为s=kt+b,代入后得到方程组,解方程组即可;
(3)先求出从甲地到乙地的总路程,现求小华的速度,然后分三种情况讨论两人在途中相遇问题.当![]() 时, 10t=10(t-1);当
时, 10t=10(t-1);当![]() 时, 20=10(t-1);当
时, 20=10(t-1);当![]() 时, 15t-40=10(t-1);逐一求解即可.
时, 15t-40=10(t-1);逐一求解即可.
解:(1)由图象可知:小明从第2小时到第4小时行驶的路程没有发生变化,所以途中停留了2![]() ;
;
由图象可知:小明2小时内行驶的路程是20 km,
所以他的速度是![]() (km/ h);
(km/ h);
故答案是:2;10.
(2)设线段![]() 的函数表达式为s=kt+b,
的函数表达式为s=kt+b,
由图象可知:B(4,20),C(5,35),
∴![]() ,
,
∴![]() ,
,
∴线段![]() 的函数表达式为s=15t-40
的函数表达式为s=15t-40![]() ;
;
(3)在s=15t-40中,当t=6时,s=15×6-40=50,
∴从甲地到乙地全程为50 km,
∴小华的速度=![]() (km/ h),
(km/ h),
下面分三种情况讨论两人在途中相遇问题:
当![]() 时,两人在途中相遇,则
时,两人在途中相遇,则
10t=10(t-1),方程无解,不合题意,舍去;
当![]() 时,两人在途中相遇,则
时,两人在途中相遇,则
20=10(t-1),解得t=3;
当![]() 时,两人在途中相遇,则
时,两人在途中相遇,则
15t-40=10(t-1),解得t=6;
∴综上所述,当t=3h或t=6h时,两人在途中相遇.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案