题目内容
【题目】已知△ABC和△CDE都为等腰直角三角形,∠ACB=∠ECD=90°.
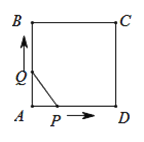
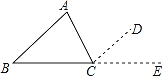
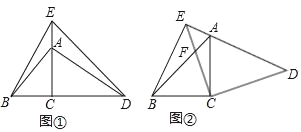
探究:如图①,当点A在边EC上,点C在线段BD上时,连结BE、AD.求证:BE=AD,BE⊥AD.
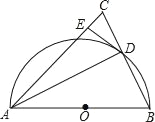
拓展:如图②,当点A在边DE上时,AB、CE交于点F,连结BE.若AE=2,AD=4,则![]() 的值为 .
的值为 .
【答案】(1)见解析;(2)![]()
【解析】
(1)根据等腰三角形得BC=CA,EC=CD,证明△BCE≌△ACD,根据同角的余角相等即可证明,(2)作辅助线证明FM=FN,根据S△ABE=S△BEF+S△AEF,求出EF,FC的长即可求![]() 的值.
的值.
解:(1)探究:延长DA交BE于F.
∵△ABC和△CDE都为等腰直角三角形,∠ACB=∠ECD=90°.
∴BC=CA,EC=CD,
∴△BCE≌△ACD,
∴BE=AD,∠BEC=∠ADC,
∵∠ACB=90°,
∴∠BEC+∠EBC=90°,
∴∠ADC+∠EBC=90°,
∴∠BFD=90°,
∴BE⊥AD.
(2)拓展:作FM⊥DE于M,FN⊥BE于N.
由探究可知:BE⊥DE,BE=AD=4,∠FEM=∠FEB=45°,
∵FM⊥DE于M,FN⊥BE于N.
∴FM=FN,
∵![]() EBFN+
EBFN+![]() AEFM=
AEFM=![]() BEAE,
BEAE,
∴FM=FN=![]() ,
,
∴EF=![]() ,
,
∵CE=CD=3![]() ,
,
∴CF=![]() ,
,
∴EF:CF=4:5.
故答案为![]() .
.

练习册系列答案
相关题目