题目内容
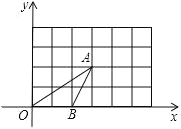
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+3a过点A(﹣1,0).
(1)求抛物线的对称轴;
(2)直线y=x+4与y轴交于点B,与该抛物线对称轴交于点C.如果该抛物线与线段BC有交点,结合函数的图象,求a的取值范围.
【答案】(1)抛物线的对称轴为x=﹣2;(2)a≥![]() 或a≤﹣2.
或a≤﹣2.
【解析】
(1)根据坐标轴上点的坐标特征代入点A的坐标,得出b=4a,则解析式为y=ax2+4ax+3a,进一步求得抛物线的对称轴;
(2)结合图形,分两种情况:①a>0;②a<0;进行讨论即可求解.
(1)∵抛物线y=ax2+bx+3a过点A(﹣1,0),
∴a﹣b+3a=0,
∴b=4a,
∴抛物线的解析式为y=ax2+4ax+3a,
∴抛物线的对称轴为x=﹣![]() =﹣2;
=﹣2;
(2)∵直线y=x+4与y轴交于点B,与该抛物线对称轴交于点C,
∴B(0,4),C(﹣2,2),
∵抛物线y=ax2+bx+3a经过点A(﹣1,0)且对称轴x=﹣2,
由抛物线的对称性可知抛物线也一定过A的对称点(﹣3,0),
①a>0时,如图1,
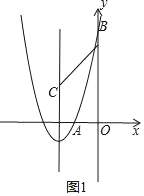
将x=0代入抛物线得y=3a,
∵抛物线与线段BC恰有一个公共点,
∴3a≥4,
解得a≥![]() ,
,
②a<0时,如图2,
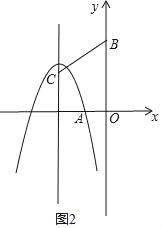
将x=﹣2代入抛物线得y=﹣a,
∵抛物线与线段BC恰有一个公共点,
∴﹣a≥2,
解得a≤﹣2;
综上所述,a≥![]() 或a≤﹣2.
或a≤﹣2.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目