Question

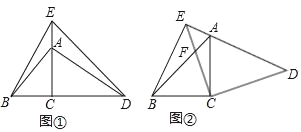
【题目】如图所示：在△ABC中，AB=AC=5，BC=8，D，E分别为BC．AB边上一点，∠ADE=∠C，

(1)求证：AD2=AEAB；

(2)∠ADC与∠BED是否相等？请说明理由；

(3)若CD=2，求AD的长．

Answer 1

【答案】(1)证明见解析；(2)∠ADC=∠BED，理由见解析；(3)AD=2.

【解析】

（1）证明△DAE∽△BAD，根据相似三角形的性质证明；
（2）根据三角形的外角的性质、等腰三角形的性质证明；
（3）证明△ADC∽△DEB，根据相似三角形的性质求出BE，代入（1）的结论计算即可．

(1)∵∠ADE=∠C，∠DAE=∠BAD，

∴△DAE∽△BAD，

∴ = ，即AD2=AEAB

(2)∠ADC=∠DAE+∠B，∠BED=∠DAE+∠ADE，

∵AB=AC，

∴∠B=∠C，

∴∠ADC=∠BED

(3)∵∠ADC=∠BED，∠B=∠C，

∴△ADC∽△DEB，

∴ = ，

即 = ，

解得，BE=2.4，

由(1)得，AD2=AEAB=12，

则AD=2