题目内容

【题目】如图，在中，，，，与的平分线交于点，过点作于点，若则的长为( )

A.B.2C.D.4

【答案】B

【解析】

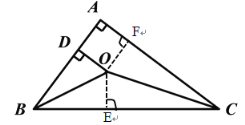
过点O作OE⊥BC于E，OF⊥AC于F，由角平分线的性质得到OD=OE=OF，根据勾股定理求出BC的长，易得四边形ADFO为正方形，根据线段间的转化即可得出结果.

解：过点O作OE⊥BC于E，OF⊥AC于F，

∵BO,CO分别为∠ABC，∠ACB的平分线，

所以OD=OE=OF，

又BO=BO,

∴△BDO≌△BEO,∴BE=BD.

同理可得，CE=CF.

又四边形ADOE为矩形，∴四边形ADOE为正方形.

∴AD=AF.

∵在Rt△ABC中，AB=6，AC=8，∴BC=10.

∴AD+BD=6①,

AF+FC=8②，

BE+CE=BD+CF=10③，

①+②得，AD+BD+AF+FC=14，即2AD+10=14，

∴AD=2.

故选：B.

练习册系列答案
相关题目

【题目】数学概念：百度百科上这样定义绝对值函数：y＝│x│＝

并给出了函数的图像（如图）．

方法迁移

借鉴研究正比例函数y＝kx与一次函数y＝kx＋b（k，b是常数，且k≠0）之间关系的经验，我们来研究函数y＝│x＋a│（a是常数）的图像与性质．

“从‘1’开始”

我们尝试从特殊到一般，先研究当a＝1时的函数y＝│x＋1│．

按照要求完成下列问题：

（1）观察该函数表达式，直接写出y的取值范围；

（2）通过列表、描点、画图，在平面直角坐标系中画出该函数的图像．

“从‘1’到一切”

（3）继续研究当a的值为－2，－，2，3，…时函数y＝│x＋a│的图像与性质，

尝试总结：

①函数y＝│x＋a│（a≠0）的图像怎样由函数y＝│x│的图像平移得到？

②写出函数y＝│x＋a│的一条性质．

知识应用

（4）已知A（x1，y1），B（x2，y2）是函数y＝│x＋a│的图像上的任意两点，且满足x1＜x2≤－1时， y1＞y2，则a的取值范围是 ．

【题目】如图，矩形ABCD 和正方形ECGF，其中E、H分别为AD、BC中点，连结AF、HG、AH.

（1）求证：；

（2）求证：；

【题目】在中，，是边上不同于、的一动点，过作，垂足为，连接．

试说明不论点在边上何处时，都有与相似；

若，，当为何值时，面积最大，并求出最大值；

在中，两条直角边、满足关系式，是否存在一个的值，使既与全等，也与全等．

【题目】如图，在四边形ABCD中，BD为一条对角线，AD∥BC，AD=2BC，∠ABD=90°，E为AD的中点，连接BE．

（1）求证：四边形BCDE为菱形；

（2）连接AC，若AC平分∠BAD，BC=1，求AC的长．

【题目】（本题满分8分）如图，四边形ABCD中，,E是边CD的中点，连接BE并延长与AD的延长线相较于点F．

（1）求证：四边形BDFC是平行四边形；

（2）若△BCD是等腰三角形，求四边形BDFC的面积．

【题目】问题提出：

(1)如图①，若正方形的边长为6，点分别为边上的点，且，与交于点，连接，则 ；

问题探究：

(2)如图②，，是等腰直角三角形，顶点分别在的两边上，试说明点在的平分线上；

问题解决：

(3)如图③，，是等边三角形，顶点分别在的两边上，点在上，且，连接，求的最小值．

【题目】中，，点为三条角平分线的交点，于，于，于，且，，，则点到三边、、的距离为（ ）

A. 2cm，2cm，2cm B. 3cm，3cm，3cm

C. 4cm，4cm，4cm D. 2cm，3cm，5cm

【题目】阅读下列材料:利用完全平方公式，将多项式变形为的形式.

例如：.

（1）填空：将多项式变形为的形式，并判断与0的大小关系.

∵.

所以______0（填“＞”、“＜”、“＝”）

（2）如图①所示的长方形边长分别是、，求长方形的面积 （用含的式子表示）；如图②所示的长方形边长分别是、，求长方形的面积 （用含的式子表示）

（3）比较（2）中与的大小，并说明理由.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网