Question

【题目】如图，在Rt△ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm.动点M从点B出发，在线段BA上以每秒3cm的速度点A运动，同时动点N从点C出发，在线段CB上以每秒2cm的速度向点B运动，其中一点到达终点后，另一点也停止运动.运动时间为t秒，连接MN.

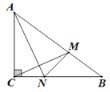
（1）填空：BM= cm.BN= cm.（用含t的代数式表示）

（2）若△BMN与△ABC相似，求t的值；

（3）连接AN，CM，若AN⊥CM，求t的值．

Answer 1

【答案】（1）3t， 8-2t；（2）△BMN与△ABC相似时，t的值为s或s；（3）t的值为.

【解析】

（1）根据“路程=时间×速度”和线段的和与差即可得；

（2）由两三角形相似得出对应线段成比例，再结合题（1）的结果，联立求解即可；

（3）如图（见解析），过点M作于点D，易证，利用相似三角形的性质求出CD和DM的长，再证，从而可建立一个关于t的等式，求解即可得.

（1）由“路程=时间×速度”得：

故答案为：；

（2）

当时，，即，解得

当时，，即，解得

综上所述，与相似时，t的值为或；

（3）如图，过点M作于点D

又∵∠B＝∠B

，

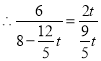解得：或（不符题意，舍去），

经检验是方程的解，

故t的值为.