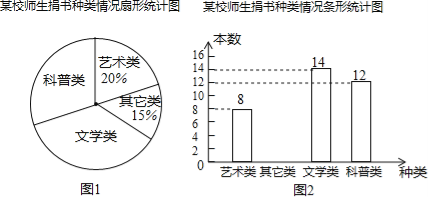
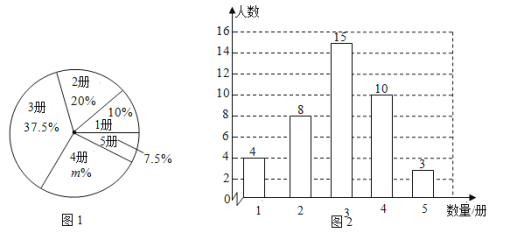
题目内容
【题目】如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC=_____________________.
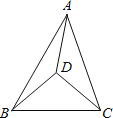
【答案】100°
【解析】
如果延长BD交AC于E,由三角形的一个外角等于与它不相邻的两个内角的和,得∠BDC=∠DEC+∠ECD,∠DEC=∠ABE+∠BAE,所以∠BDC=∠ABE+∠BAE+∠ECD,又DA=DB=DC,根据等腰三角形等边对等角的性质得出∠ABE=∠DAB=20°,∠ECD=∠DAC=30°,进而得出结果.
解:延长BD交AC于E.
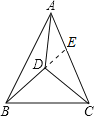
∵DA=DB=DC,
∴∠ABE=∠DAB=20°,∠ECD=∠DAC=30°.
又∵∠BAE=∠BAD+∠DAC=50°,
∠BDC=∠DEC+∠ECD,∠DEC=∠ABE+∠BAE,
∴∠BDC=∠ABE+∠BAE+∠ECD=20°+50°+30°=100°.
故答案为:100°.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目