题目内容
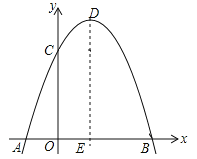
【题目】如图,过点A(﹣1,0)、B(3,0)的抛物线y=﹣x2+bx+c与y轴交于点C,它的对称轴与x轴交于点E.
(1)求抛物线解析式;
(2)求抛物线顶点D的坐标;
(3)若抛物线的对称轴上存在点P使S△PCB=3S△POC,求此时DP的长.
【答案】(1)抛物线解析式为y=﹣x2+2x+3;
(2)顶点D的坐标为(1,4);
(3)DP的长为1或5.
【解析】
试题分析:(1)利用待定系数法即可求得解析式;
(2)把抛物线解析式化成顶点式,即可得出顶点坐标;
(3)求出△POC的面积,由三角形的面积关系得出PF=3,求出直线BC的解析式,得出F的坐标,再分两种情况讨论,即可得出DP的长.
试题解析:(1)将A(﹣1,0),B(3,0)代入y=﹣x2+bx+c得:![]() ,
,
解得:b=2,c=3,∴抛物线解析式为y=﹣x2+2x+3;
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点D的坐标为(1,4);
(3)设BC与抛物线的对称轴交于点F,如图所示:

则点F的横坐标为1,
∵y=﹣x2+2x+3,
当x=0时,y=3,∴OC=3,∴△POC的面积=![]() ×3×1=
×3×1=![]() ,
,
∵△PCB的面积=△PCF的面积+△PBF的面积=![]() PF(1+2)=3×
PF(1+2)=3×![]() ,解得:PF=3,
,解得:PF=3,
设直线BC的解析式为y=kx+a,则![]() ,解得:a=3,k=﹣1,∴直线BC的解析式为y=﹣x+3,
,解得:a=3,k=﹣1,∴直线BC的解析式为y=﹣x+3,
当x=1时,y=2,
∴F的坐标为(1,2),∴EF=2,
当点P在F的上方时,PE=PF+EF=5,∴DP=5﹣4=1;
当点P在F的下方时,PE=PF﹣EF=3﹣2=1,∴DP=4+1=5;
综上所述:DP的长为1或5.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目