题目内容
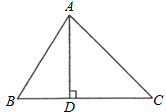
【题目】如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°,AC=![]() ,
,
(1)求AD的长. (2)求⊿ABC的面积。
【答案】(1)3;(2)![]()
【解析】试题分析:(1)根据三角形内角和可得∠DAC=45°,根据等角对等边可得AD=CD,然后再根据勾股定理可计算出AD的长;
(2)根据三角形内角和可得∠BAD=30°,再根据直角三角形的性质可得AB=2BD,然后利用勾股定理计算出BD的长,进而可得BC的长,然后利用三角形的面积公式计算即可.
试题解析:(1)∵∠C=45°,AD是△ABC的边BC上的高,
∴∠DAC=45°,
∴AD=CD,
∵AC2=AD2+CD2,
∴(![]() )2=2AD2,
)2=2AD2,
∴AD=3;
(2)在Rt△ADB中,∵∠B=60°,
∴∠BAD=30°,
∴AB=2BD,
∵AB2=BD2+AD2,
∴(2BD)2=BD2+AD2,
3BD2=9,
BD=![]() ,
,
∴△ABC的面积: ![]() BCAD=
BCAD=![]() (BD+DC)AD=
(BD+DC)AD=![]() ×(
×(![]() +3)×3=
+3)×3=![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目