题目内容
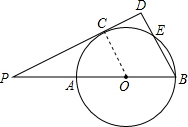
如图，已知PAB是⊙O的割线，AB为⊙O的直径，PC为⊙O的切线，C为切点，BD⊥PC于点D，交⊙O于点E，PA=AO=OB=1．
（Ⅰ）求∠P的度数；
（Ⅱ）求DE的长．
（Ⅰ）求∠P的度数；
（Ⅱ）求DE的长．
（1）连接OC
∵OC⊥PD
∴OC=OA=1
在Rt△OPC中
OC=1，OP=2
∴sin∠P=
=
∴∠P=30°；
（2）在Rt△POC中
OP=2，OC=1
∴PC=
=
=
∵OC⊥PD，BD⊥PC
∴△POC∽△PBD
即
=
=
∴
=
=
解得PD=
，BD=
∴CD=PD-PC=
-
=
∵CD2=DE•BD
∴（
）2=DE•
解得DE=
．
∵OC⊥PD
∴OC=OA=1
在Rt△OPC中
OC=1，OP=2
∴sin∠P=
| OC |
| OP |
| 1 |
| 2 |
∴∠P=30°；
（2）在Rt△POC中
OP=2，OC=1
∴PC=
| OP2-OC2 |
| 22-12 |
| 3 |
∵OC⊥PD，BD⊥PC
∴△POC∽△PBD
即
| PC |
| PD |
| OC |
| BD |
| OP |
| PB |
∴
| ||
| PD |
| 1 |
| BD |
| 2 |
| 3 |
解得PD=
3
| ||
| 2 |
| 3 |
| 2 |
∴CD=PD-PC=
3
| ||
| 2 |
| 3 |
| ||
| 2 |
∵CD2=DE•BD
∴（
| ||
| 2 |
| 3 |
| 2 |
解得DE=
| 1 |
| 2 |
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
