题目内容
圆外切等腰梯形的底角为30°,中位线的长为8,则该圆的直径长为______.
根据题意画出相应的图形,过A作AM⊥BC于M点,如图所示:
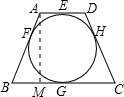
∵梯形ABCD的中位线为8,
∴AD+BC=2×8=16,
即AE+ED+BG+GC=16,
又梯形为圆的外切梯形,
∴梯形各边与圆相切,
∴AE=AF,DE=DH,BF=BG,CG=CH,
∴AF+FB+DH+HC=16,即AB+CD=16,
又梯形ABCD为等腰梯形,
∴AB=CD=8,
在Rt△ABM中,∠B=30°,∠AMB=90°,AB=8,
则AM=
AB=4,即圆的直径为4.
故答案为:4

∵梯形ABCD的中位线为8,
∴AD+BC=2×8=16,
即AE+ED+BG+GC=16,
又梯形为圆的外切梯形,
∴梯形各边与圆相切,
∴AE=AF,DE=DH,BF=BG,CG=CH,
∴AF+FB+DH+HC=16,即AB+CD=16,
又梯形ABCD为等腰梯形,
∴AB=CD=8,
在Rt△ABM中,∠B=30°,∠AMB=90°,AB=8,
则AM=
| 1 |
| 2 |
故答案为:4

练习册系列答案
相关题目