Question

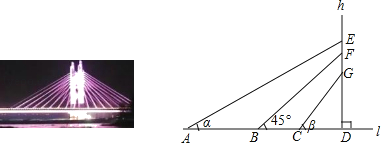
【题目】如图，是一座横跨沙颖河的斜拉桥，拉索两端分别固定在主梁l和索塔h上，索塔h垂直于主梁l，垂足为D．拉索AE，BF，CG的仰角分别是α，45°，β，且α+β＝90°（α＜β），AB＝15m，BC＝5m，CD＝4m，EF＝3FG，求拉索AE的长．（精确到1m，参考数据：≈2.24，≈1.41）

Answer 1

【答案】拉索AE的长约为27m

【解析】

证出△BDF是等腰直角三角形，得出FD＝BD＝BC+CD＝9m，证明△ADE∽△GDC，得出，则ADCD＝GDED，设EF＝3FG＝3x，则24×4＝（9﹣x）（9+3x），解得EF＝3，得出DE＝EF+FD＝12m，由勾股定理求出AE即可．

解：在Rt△BDF中，∵∠DBF＝45°，∠BDF＝90°，

∴△BDF是等腰直角三角形，

∴FD＝BD＝BC+CD＝9m，

∵α+β＝90°，∠ADE＝∠GDC＝90°，

∴△ADE∽△GDC，

∴，

∴ADCD＝GDED，

设EF＝3FG＝3x，则24×4＝（9﹣x）（9+3x），

解得：x＝1，或x＝5（舍去），

∴EF＝3，

∴DE＝EF+FD＝12m，

∵AD＝AB+BD＝24m，

∴AE＝≈27（m），

答：拉索AE的长约为27m．