Question

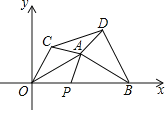
【题目】如图，在平面直角坐标系中，A（，1），B（2，0），点P为线段OB上一动点，将△AOP沿AO翻折得到△AOC，将△ABP沿AB翻折得到△ABD，则△ACD面积的最小值为_____．

Answer 1

【答案】

【解析】

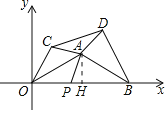
如详解图，作AH⊥OB于H．首先证明∠OAB＝120°，再证明△CAD是顶角为120°的等腰三角形，最后根据垂线段最短解决问题即可．

解：如图，作AH⊥OB于H．

∵A（，1），

∴OH＝，AH＝1，

∴tan∠OAH＝＝，

∴∠OAH＝60°，

∵B（2，0），

∴OH＝HB＝，

∵AH⊥OB，

∴AO＝AB，

∴∠OAH＝∠BAH＝60°，

由翻折的性质可知：AP＝AC＝AD，∠PAO＝∠CAO，∠BAP＝∠BAD，

∴∠OAC+∠BAD＝∠OAB＝120°，

∴∠CAD＝360°﹣2×120°＝120°，

∴△CAD是顶角为120°的等腰三角形，

根据垂线段最短可知，当AP与AH重合时，AC＝AD＝PA＝1，

此时△ACD的面积最小，最小值＝×1×1sin60°＝．

故答案为．