题目内容
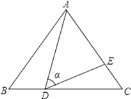
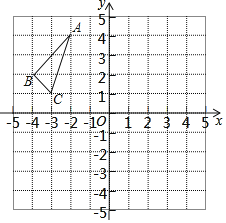
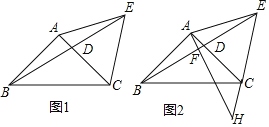
【题目】如图1,在△ABC中,AB=AC,∠BAC=90°,D为AC边上一动点,且不与点A点C重合,连接BD并延长,在BD延长线上取一点E,使AE=AB,连接CE.
(1)若∠AED=20°,则∠DEC= 度;
(2)若∠AED=a,试探索∠AED与∠AEC有怎样的数量关系?并证明你的猜想;
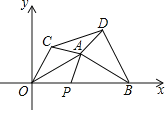
(3)如图2,过点A作AF⊥BE于点F,AF的延长线与EC的延长线交于点H,求证:EH2+CH2=2AE2.
【答案】(1)45度;(2)∠AEC﹣∠AED=45°,理由见解析;(3)见解析
【解析】
(1)由等腰三角形的性质可求∠BAE=140°,可得∠CAE=50°,由等腰三角形的性质可得∠AEC=∠ACE=65°,即可求解;
(2)由等腰三角形的性质可求∠BAE=180°﹣2α,可得∠CAE=90°﹣2α,由等腰三角形的性质可得∠AEC=∠ACE=45°+α,可得结论;
(3)如图,过点C作CG⊥AH于G,由等腰直角三角形的性质可得EH=![]() EF,CH=
EF,CH=![]() CG,由“AAS”可证△AFB≌△CGA,可得AF=CG,由勾股定理可得结论.
CG,由“AAS”可证△AFB≌△CGA,可得AF=CG,由勾股定理可得结论.
解:(1)∵AB=AC,AE=AB,
∴AB=AC=AE,
∴∠ABE=∠AEB,∠ACE=∠AEC,
∵∠AED=20°,
∴∠ABE=∠AED=20°,
∴∠BAE=140°,且∠BAC=90°
∴∠CAE=50°,
∵∠CAE+∠ACE+∠AEC=180°,且∠ACE=∠AEC,
∴∠AEC=∠ACE=65°,
∴∠DEC=∠AEC﹣∠AED=45°,
故答案为:45;
(2)猜想:∠AEC﹣∠AED=45°,
理由如下:∵∠AED=∠ABE=α,
∴∠BAE=180°﹣2α,
∴∠CAE=∠BAE﹣∠BAC=90°﹣2α,
∵∠CAE+∠ACE+∠AEC=180°,且∠ACE=∠AEC,
∴∠AEC=45°+α,
∴∠AEC﹣∠AED=45°;
(3)如图,过点C作CG⊥AH于G,

∵∠AEC﹣∠AED=45°,
∴∠FEH=45°,
∵AH⊥BE,
∴∠FHE=∠FEH=45°,
∴EF=FH,且∠EFH=90°,
∴EH=![]() EF,
EF,
∵∠FHE=45°,CG⊥FH,
∴∠GCH=∠FHE=45°,
∴GC=GH,
∴CH=![]() CG,
CG,
∵∠BAC=∠CGA=90°,
∴∠BAF+∠CAG=90°,∠CAG+∠ACG=90°,
∴∠BAF=∠ACG,且AB=AC,∠AFB=∠AGC,
∴△AFB≌△CGA(AAS)
∴AF=CG,
∴CH=![]() AF,
AF,
∵在Rt△AEF中,AE2=AF2+EF2,
∴(![]() AF)2+(
AF)2+(![]() EF)2=2AE2,
EF)2=2AE2,
∴EH2+CH2=2AE2.