题目内容
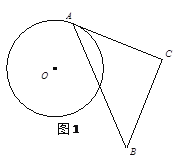
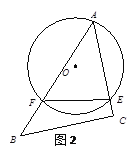
【题目】问题提出：如图，已知：线段AB，试在平面内找到符合条件的所有点C，
使∠ACB=30°。（利用直尺和圆规作图，保留作图痕迹，不写作法)．
尝试解决：为了解决这个问题，下面给出一种解题思路：先作出等边三角形AOB，然后以点O 为圆心，OA长为半径作⊙O，则优弧AB上的点即为所要求作的点（点A、B除外），根据对称性，在AB的另一侧符合条件的点C易得。请根据提示，完成作图.
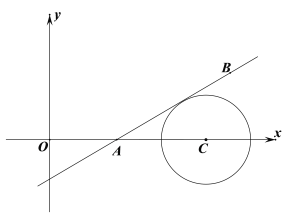
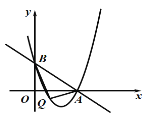
自主探索：在平面直角坐标系中，已知点A(3，0)、B(－1，0)，点C是y轴上的一个动点，当∠BCA=45°时，点C的坐标为 .
【答案】（1）如图1，两段优弧（不含A、B两端点）为所作；见解析；(2) 满足条件的C点坐标为C（0，2+
）或（0，-2-）．
【解析】
（1）利用题中的思路画出两段优弧即可；
（2）以类似（1）的方法作出满足条件的C点，如图2，然后利用勾股定理计算出CD的长，从而确定C的坐标，利用对称再得到
坐标即可.
（1）如图1，两段优弧（不含A、B两端点）为所作；
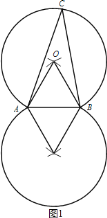
(2)
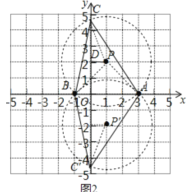
先做等腰直角△PAB，再以P点为圆心，PA为半径作圆O交y轴于C点；
作PD⊥y轴于D，易得P（1,2），PA=
∴PC=
∴CD=
∴OC=2＋
∴C（0,2＋）
同理可得（0，-2-）
综上所述，满足条件的C点坐标为C（0，2+）或（0，-2-）．
练习册系列答案
相关题目
