题目内容
【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F. 
(1)求证:△ABE≌△CDF;
(2)若AB=DB,猜想:四边形DFBE是什么特殊的四边形?并说明理由.
【答案】
(1)证明:∵四边形ABCD是平行四边形
AB=CD,∠A=∠C.
AB∥CD,∴∠ABD=∠CDB.
∵BE平分∠ABD,DF平分∠CDB,
∴∠ABE=∠ABD,∠CDF=∠CDB.
∴∠ABE=∠CDF.
在△ABE和△CDF中, 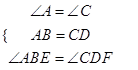
∴△ABE≌△CDF(SAS)
(2)解:四边形DFBE是矩形.理由如下:
∵AB=DB,BE平分∠ABD,
∴BE⊥AD,即∠DEB=90°.
∵AB=DB,AB=CD,
∴DB=CD.
∵DF平分∠CDB,
∴DF⊥BC,即∠BFD=90°.
在□ABCD中,∵AD∥BC,
∴∠EDF+∠DEB=180°.
∴∠EDF=90°.
∴∠DEB=∠BFD=∠EDF=90°.
∴四边形DFBE是矩形
【解析】(1)首先利用平行四边形的想得到AB=CD,∠A=∠C,再利用角平分线的性质得到∠ABE=∠CDF,利用ASA证明△ABE≌△CDF;(2)证明∠DEB=∠BFD=∠EDF=90°.即可解决问题.
【考点精析】本题主要考查了平行四边形的性质和矩形的判定方法的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形才能正确解答此题.

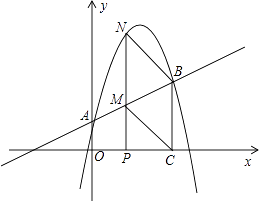
【题目】如图,已知二次函数y=ax2+bx+c的图象如图所示,则下列四个结论:①a+b+c<0;②a+c=b;③b=﹣2a;④4ac﹣b2<0,其中正确的结论有( ) 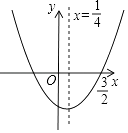
A.4个
B.3个
C.2个
D.1个
【题目】(本小题满分18分)某校八(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量 | 频数(户) | 频率 |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
| 2 | 0.04 |
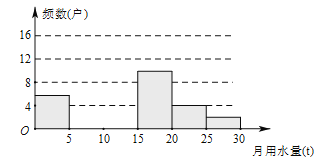
请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)若该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20 t的家庭大约有多少户?