题目内容
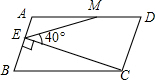 如图,在平行四边形ABCD中,AD=2AB,M是AD的中点,CE⊥AB于点E,∠CEM=40°,则∠DME是( )
如图,在平行四边形ABCD中,AD=2AB,M是AD的中点,CE⊥AB于点E,∠CEM=40°,则∠DME是( )| A、150° | B、140° | C、135° | D、130° |
分析:添加辅助线,构造△MDF,利用角边角证明△AME与△FMD全等,得到M为EF的中点,根据平行四边形的对边平行,得到∠BEC等于∠ECF都为直角,根据直角三角形斜边上的中线等于斜边的一半,得出ME和MC相等,根据等比对等角,得到∠MEC等于∠MCE都等于40°,从而得出∠EMC和∠MCD的度数,再根据AD等于AB的二倍,AD等于MD的二倍,所以MD等于AB,根据平行四边形的性质得AB=CD,即MD=CD,根据等边对等角求出∠DMC的度数,而要求的角等于上边求出的∠EMC和∠DMC的和,从而求出答案.
解答: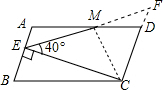 解:延长EM与CD的延长线交于点F,连接CM,
解:延长EM与CD的延长线交于点F,连接CM,
∵M是AD的中点,∴AM=DM,
∵ABCD为平行四边形,
∴AB∥CD,又∠BEC=90°,
∴∠ECF=90°,∠A=MDF,又∠AME=∠DMF,
∴△AEM≌△DFM,
∴EM=FM,
∴CM=EM=
EF,
∴∠MEC=∠MCE=40°,
∴∠EMC=100°,∠MCD=50°,
又∵M为AD中点,AD=2DC,
∴MD=CD=
AD,
∴∠DMC=∠DCM=50°,
∴∠DME=∠EMC+∠DMC=100°+50°=150°.
故选A
 解:延长EM与CD的延长线交于点F,连接CM,
解:延长EM与CD的延长线交于点F,连接CM,∵M是AD的中点,∴AM=DM,
∵ABCD为平行四边形,
∴AB∥CD,又∠BEC=90°,
∴∠ECF=90°,∠A=MDF,又∠AME=∠DMF,
∴△AEM≌△DFM,
∴EM=FM,
∴CM=EM=
| 1 |
| 2 |
∴∠MEC=∠MCE=40°,
∴∠EMC=100°,∠MCD=50°,
又∵M为AD中点,AD=2DC,
∴MD=CD=
| 1 |
| 2 |
∴∠DMC=∠DCM=50°,
∴∠DME=∠EMC+∠DMC=100°+50°=150°.
故选A
点评:此题考查了学生平行四边形的性质以及直角三角形的性质,同时还要注意等腰三角形的性质在做题中的灵活运用,这道题往往会作为中考时填空题或选择题方面的压轴题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平行四边形ABCD中,AB=2
如图,在平行四边形ABCD中,AB=2| 2 |
| 3 |
| 5 |
| A、AC⊥BD |
| B、四边形ABCD是菱形 |
| C、△ABO≌△CBO |
| D、AC=BD |
 17、如图,在平行四边形ABCD中,EF∥AD,GH∥AB,EF、GH相交于点O,则图中共有
17、如图,在平行四边形ABCD中,EF∥AD,GH∥AB,EF、GH相交于点O,则图中共有 如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,证明:四边形DFBE是平行四边形.
如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,证明:四边形DFBE是平行四边形. 的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米.
的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米. (2013•同安区一模)如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为
(2013•同安区一模)如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为