Question

【题目】已知：

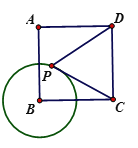
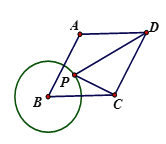
图1 图2 图3

（1）初步思考：

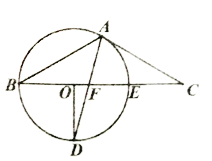
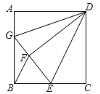
如图1， 在中，已知，BC=4，N为BC上一点且，试说明：

（2）问题提出：

如图2，已知正方形ABCD的边长为4，圆B的半径为2，点P是圆B上的一个动点，求的最小值．

（3）推广运用：

如图3，已知菱形ABCD的边长为4，∠B﹦60°，圆B的半径为2，点P是圆B上的一个动点，求的最大值．

Answer 1

【答案】（1）详见解析；（2）5；（3）最大值

【解析】

（1）利用两边成比例，夹角相等，证明∽，得到，即可得到结论成立；

（2）在BC上取一点G，使得BG=1，由△PBG∽△CBP，得到，当D、P、G共线时，的值最小，即可得到答案；

（3）在BC上取一点G，使得BG=1，作DF⊥BC于F，与（2）同理得到，当点P在DG的延长线上时，，即可得到答案.

（1）证明：∵，

∴，

∴，

∴，

∵，

∴，

∴，

∴；

（2）解：如图，在BC上取一点G，使得BG=1，

∵，

∴，

∴，

∴，

∴，

∴；

∵，

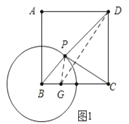
∴当D、P、G共线时，的值最小，

∴最小值为：；

（3）如图，在BC上取一点G，使得BG=1，作DF⊥BC于F，

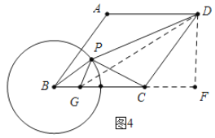
与（2）同理，可证，

在Rt△CDF中，∠DCF=60°，CD=4，
∴DF=CDsin60°=，CF=2，
在Rt△GDF中，DG=，

∴，

当点P在DG的延长线上时，，

∴最大值为：.