Question

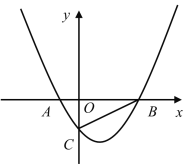
【题目】如图，已知二次函数与轴交于、两点（点在点左），与轴交于点，连接，点为二次函数图象上的动点．

（1）若的面积为3，求抛物线的解析式；

（2）在（1）的条件下，若在轴上存在点，使得，求点的坐标；

（3）若为对称轴右侧抛物线上的动点，直线交轴于点，直线交轴于点，判断的值是否为定值，若是，求出定值，若不是请说明理由．

Answer 1

【答案】（1）；（2）（-2，）或（6，）；（3）的值为定值

【解析】

（1）令y=0，求出点A和点B的坐标，得到AB和OC，再根据△ABC的面积求出a的值；

（2）分当点F在y轴正半轴时，当点F在y轴负半轴两种情况，过点P作y轴垂线于点Q，设点P坐标为（x，），证明△PQC∽△COB，通过比例关系求出点P的横坐标，从而得出结果；

（3）设PA的解析式为：y=kx+k，PB的解析式为：y=mx-3m，分别和抛物线表达式联立，利用根与系数的关系得出点P横坐标的两种表示方法，再根据函数表达式得出点C、D、E的坐标，得到EC和DE的长，从而证明为定值.

解：（1）令y=0，则，

解得：x1=-1，x2=3，

∴A（-1，0），B（3，0），

∴AB=4，OC=-3a，

∴S△ABC=，

解得a=，

∴抛物线的表达式为；

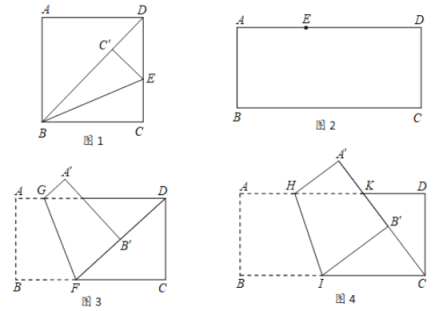
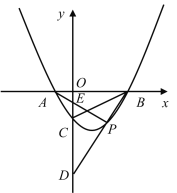
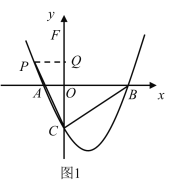
（2） 如图1、2，当点F在y轴正半轴时，

过点P作y轴垂线于点Q，

∵∠PCF=∠ABC，∠PQC=∠BOC，

∴△PQC∽△COB，

∴，

设点P坐标为（x，），

∴图1中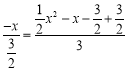，，解得：x=-2或0（舍），

图2中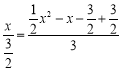，，解得：x=6或0（舍），

代入抛物线表达式中可得：

点P的坐标为（-2，）或（6，）；

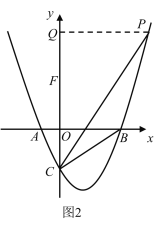
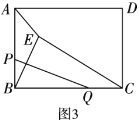
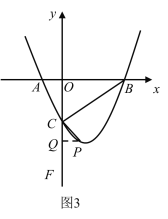
如图3，当点F在y轴负半轴时，过点P作y轴垂线于点Q，

同理可知：△PQC∽△COB，

则，设点P坐标为（x，），

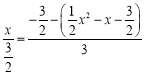∴，解得：x=-2或0，

由于此时点P只能在y轴右侧，所以x≠-2，

综上：点P的坐标为（-2，）或（6，）；

（3）∵A（-1，0），B（3，0），

设PA的解析式为：y=kx+k，PB的解析式为：y=mx-3m，

联立：，，

可得：，，

∴点P的横坐标为或，且=，

∴m-k=4a，即k=m-4a，

E（0，k），D（0，-3m），C（0，-3a），

∴EC=k+3a，DE=k+3m，

∴，

故的值为定值.