题目内容
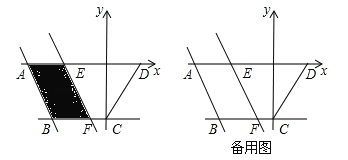
【题目】如图,在平面直角坐标系中,四边形ABCD的边AD在x轴上,点C在y轴的负半轴上,直线BC∥AD,且BC=3,OD=2,将经过A、B两点的直线l:y=﹣2x﹣10向右平移,平移后的直线与x轴交于点E,与直线BC交于点F,设AE的长为t(t≥0).
(1)四边形ABCD的面积为 ;
(2)设四边形ABCD被直线l扫过的面积(阴影部分)为S,请直接写出S关于t的函数解析式;
(3)当t=2时,直线EF上有一动点,作PM⊥直线BC于点M,交x轴于点N,将△PMF沿直线EF折叠得到△PTF,探究:是否存在点P,使点T恰好落在坐标轴上?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)20;(2) ;(3)P(﹣6,6)或P(﹣
;(3)P(﹣6,6)或P(﹣![]() ,﹣
,﹣![]() ).
).
【解析】
试题分析:(1)根据函数解析式得到OA=5,求得AC=7,得到OC=4,于是得到结论;
(2)①当0≤t≤3时,根据已知条件得到四边形ABFE是平行四边形,于是得到S=AEOC=4t;
②当3≤t<7时,如图1,求得直线CD的解析式为:y=2x﹣4,直线E′F′的解析式为:y=﹣2x+2t﹣10,解方程组得到G的坐标,于是得到S=S四边形ABCD﹣S△DE′G;
③当t≥7时,S=S四边形ABCD=20;
(3)当t=2时,点E,F的坐标分别为(﹣3,0),(﹣1,﹣4),此时直线EF的解析式为:y=﹣2x﹣6,设动点P的直线为(m,﹣2m﹣6),求得PM=|(﹣2m﹣6)﹣(﹣4)|=2|m+1|,PN=(﹣2m﹣6|=2(m+3|,FM=|m﹣(﹣1)|=|m+1,分两种情况讨论:
①假设直线EF上存在点P,使点T恰好落在x轴上,如图2,连接PT,FT;
②假设直线EF上存在点P,使点T恰好落在y轴上,如图3,连接PT,FT,根据全等三角形的判定性质和相似三角形的判定和性质即可得到结论.
试题解析:(1)在y=﹣2x﹣10中,当y=0时,x=﹣5,∴A(﹣5,0),∴OA=5,∴AC=7,把x=﹣3代入y=﹣2x﹣10得,y=﹣4,∴OC=4,∴四边形ABCD的面积=![]() (3+7)×4=20;
(3+7)×4=20;
故答案为:20;
(2)①当0≤t≤3时,∵BC∥AD,AB∥EF,∴四边形ABFE是平行四边形,∴S=AEOC=4t;
②当3≤t<7时,如图1,∵C(0,﹣4),D(2,0),∴直线CD的解析式为:y=2x﹣4,∵E′F′∥AB,BF′∥AE′
∴BF′=AE=t,∴F′(t﹣3,﹣4),直线E′F′的解析式为:y=﹣2x+2t﹣10,解![]() 得,
得, ,∴G(
,∴G(![]() ,t﹣7),∴S=S四边形ABCD﹣S△DE′G=20﹣
,t﹣7),∴S=S四边形ABCD﹣S△DE′G=20﹣![]() ×(7﹣t)×(7﹣t)=
×(7﹣t)×(7﹣t)=![]() ,③当t≥7时,S=S四边形ABCD=20;
,③当t≥7时,S=S四边形ABCD=20;
综上所述:S关于t的函数解析式为: ;
;
(3)当t=2时,点E,F的坐标分别为(﹣3,0),(﹣1,﹣4),此时直线EF的解析式为:y=﹣2x﹣6,设动点P的直线为(m,﹣2m﹣6),∵PM⊥直线BC于M,交x轴于n,∴M(m,﹣4),N(m,0),∴PM=|(﹣2m﹣6)﹣(﹣4)|=2|m+1|,PN=(﹣2m﹣6|=2(m+3|,FM=|m﹣(﹣1)|=|m+1,分两种情况讨论:
①假设直线EF上存在点P,使点T恰好落在x轴上,如图2,连接PT,FT,则△PFM≌△PFT,∴PT=PM=2|m+1|,FT=FM=|m+1|,∴![]() =2,作FK⊥x轴于K,则KF=4,由△TKF∽△PNT得,
=2,作FK⊥x轴于K,则KF=4,由△TKF∽△PNT得,![]() =2,∴NT=2KF=8,∵PN2+NT2=PT2,∴4(m+3)2+82=4(m+1)2,解得:m=﹣6,∴﹣2m﹣6=﹣6,此时,P(﹣6,6);
=2,∴NT=2KF=8,∵PN2+NT2=PT2,∴4(m+3)2+82=4(m+1)2,解得:m=﹣6,∴﹣2m﹣6=﹣6,此时,P(﹣6,6);
②假设直线EF上存在点P,使点T恰好落在y轴上,如图3,连接PT,FT,则△PFM≌△PFT,∴PT=PM=2|m+1|,FT=FM=|m+1|,∴![]() =2,作PH⊥y轴于H,则PH=|m|,由△TFC∽△PTH得,
=2,作PH⊥y轴于H,则PH=|m|,由△TFC∽△PTH得,![]() =2,∴HT=2CF=2,∵
=2,∴HT=2CF=2,∵![]() ,即
,即![]() ,解得:m=﹣
,解得:m=﹣![]() ,m=0(不合题意,舍去),∴m=﹣
,m=0(不合题意,舍去),∴m=﹣![]() 时,﹣2m﹣6=﹣
时,﹣2m﹣6=﹣![]() ,∴P(﹣
,∴P(﹣![]() ,﹣
,﹣![]() ),综上所述:直线EF上存在点P(﹣6,6)或P(﹣
),综上所述:直线EF上存在点P(﹣6,6)或P(﹣![]() ,﹣
,﹣![]() )使点T恰好落在y轴上.
)使点T恰好落在y轴上.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
