题目内容
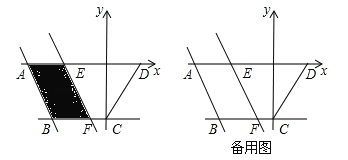
【题目】已知,直线 ![]() 与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.且点P(1,a)为坐标系中的一个动点.
与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.且点P(1,a)为坐标系中的一个动点. 
(1)求三角形ABC的面积S△ABC;
(2)请说明不论a取任何实数,三角形BOP的面积是一个常数;
(3)要使得△ABC和△ABP的面积相等,求实数a的值.
【答案】
(1)解:令 ![]() 中x=0,得点B坐标为(0,2);
中x=0,得点B坐标为(0,2);
令y=0,得点A坐标为(3,0).
由勾股定理可得 ![]() ,
,
所以S△ABC=6.5;
(2)解:不论a取任何实数,三角形BOP都可以以BO=2为底,点P到y轴的距离1为高,
所以S△BOP=1为常数;
(3)解:当点P在第四象限时,
因为 ![]() ,S△BOP=1,
,S△BOP=1,
所以 ![]() ,
,
即3﹣ ![]() a﹣1=
a﹣1= ![]() ,解得a=﹣3,
,解得a=﹣3,
当点P在第一象限时,
∵S△ABO=3,S△APO= ![]() a,S△BOP=1,
a,S△BOP=1,
∴S△ABP=S△BOP+S△AOP﹣S△ABO= ![]() ,
,
即1+ ![]() a﹣3=
a﹣3= ![]() ,
,
用类似的方法可解得 ![]() .
.

【解析】(1)先求出A、B两点的坐标,利用勾股定理得到AB的长,等腰Rt△ABC的面积为AB平方的一半;(2)三角形BOP的底边BO=2,BO边上的高为P点的横坐标1,所以它的面积是一个常数1;(3)实际上给定△ABP的面积,求P点坐标.利用面积和差求△ABP的面积,注意要分类讨论.
【考点精析】本题主要考查了一次函数的性质和三角形的面积的相关知识点,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;三角形的面积=1/2×底×高才能正确解答此题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目