Question

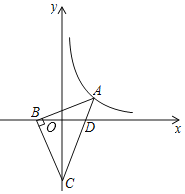
【题目】如图，在Rt△ABC中，∠ABC＝90，C（0，﹣2），AC＝3AD，点A在反比例函数y＝上，且y轴平分∠ACB，若则k＝_____．

Answer 1

【答案】

【解析】

作x轴的垂线，构造相似三角形，利用CD＝3AD和C（0，﹣2）可以求出A的纵坐标，再利用三角形相似，设未知数，由相似三角形对应边成比例，列出方程，求出待定未知数，从而确定点A的坐标，进而确定k的值．

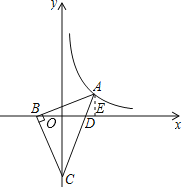
过A作AE⊥x轴，垂足为E，

∵C（0，﹣2），

∴OC＝2，

∵AC＝3AD，

∴

∵∠AED＝∠COD＝90°，∠ADE＝∠CDO

∴△ADE∽△CDO，

∴AE＝1；

又∵y轴平分∠ACB，CO⊥BD，

∴BO＝OD，

∵∠ABC＝90°，

∴∠OCD＝∠DAE＝∠ABE，

∴△ABE～△COD，

∴

设DE＝n，则BO＝OD＝2n，BE＝5n，

∴

∴n=

∴OE＝3n＝，

∴A（，1）

∴k＝×1＝．

故答案：．