题目内容
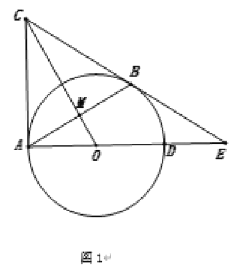
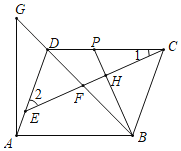
【题目】在平行四边形ABCD中，点E是AD边上一点，连接CE，交对角线BD于点F，过点A作AB的垂线交BD的延长线于点G，过B作BH垂直于CE，垂足为点H，交CD于点P，2∠1+∠2＝90°．
（1）若PH＝2，BH＝4，求PC的长；
（2）若BC＝FC，求证：GF＝
PC．
【答案】(1)2
;(2)见解析.
【解析】
（1）根据四边形ABCD是平行四边形，先证∠BCP＝∠BPC，再根据勾股定理即可求出答案；
（2）由（1）得：BC＝BP＝AD，可知四边形ABPD是等腰梯形，从而证∠1＝∠GAD，然后证△DAG≌△FCD，作FM⊥CD于M，BN⊥CD于N，△CFM≌△BPN即可求出答案.
（1）解：∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，AB∥CD，AB＝CD，
∴∠BCH＝∠2，
∴∠BCP＝∠2+∠1，
∵2∠1+∠2＝90°．
∴∠BCP＝90°﹣∠1，
∵BH⊥CE，
∴∠BPC+∠1＝90°，
∴∠BPC＝90°﹣∠1，
∴∠BCP＝∠BPC，
∴BC＝BP＝BH+PH＝4+2＝6，
∴CH2＝BC2﹣BH2＝62﹣42＝20，
∴PC＝
＝
＝2；
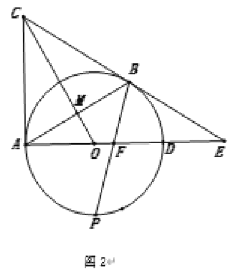
（2）证明：由（1）得：BC＝BP＝AD，
∴四边形ABPD是等腰梯形，
∴∠DAB＝∠PBA，
∵CD∥AB，
∴∠PBA＝∠BPC，
∵BH⊥CE，
∴∠1＝90°﹣∠BPC＝90°﹣∠PBA＝90°﹣∠DAB＝∠GAD，
∵AD＝BC，BC＝FC，
∴AD＝FC，∠CBF＝∠CFB，
∵AD∥BC，
∴∠EDF＝∠CBF，
∴∠EDF＝∠CFB＝∠EFD，
∴∠ADG＝∠CFD，
在△DAG和△FCD中，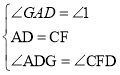
，
∴△DAG≌△FCD（ASA），
∴AG＝CD＝AB，DG＝FD，
∵AG⊥AB，
∴△ABG是等腰直角三角形，
∴∠DBA＝∠G＝45°，
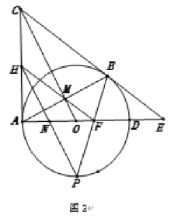
作FM⊥CD于M，BN⊥CD于N，如图所示：
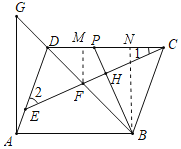
∵AB∥CD，
∴∠CDF＝∠DBA＝45°，
∴△DMF是等腰直角三角形，
∴DM＝FM，DF＝
FM，
∵BN⊥CD，BH⊥CE，
∴由三角形内角和定理得：∠1＝∠PBN，
在△CFM和△BPN中，
，
∴△CFM≌△BPN（AAS），
∴FM＝PN，
∵BC＝BP，BN⊥CD，
∴PN＝CN，
∴PC＝2PN＝2FM＝DF，
∴PC＝2DF，
∴GF＝2DF＝PC
