题目内容
【题目】解方程组、不等式组:
(1)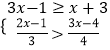
(2)![]() .
.
【答案】
(1)解: 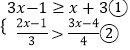
∵解不等式①得:x≥2,
解不等式②得:x<8,
∴不等式组的解集为:2≤x<8
(2)解:整理得: ![]()
①﹣②×3得:﹣10x=12.5,
解得:x=﹣1.25,
把x=﹣1.25代入②得:﹣7.5﹣3y=2.5,
y=﹣ ![]() ,
,
所以原方程组的解为: 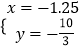
【解析】(1)先求出不等式的解集,再求出不等式组的解集即可;(2)①﹣②×3得出﹣10x=12.5,求出x,把x=﹣1.25代入②求出y即可.
【考点精析】通过灵活运用解二元一次方程组和一元一次不等式组的解法,掌握二元一次方程组:①代入消元法;②加减消元法;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )即可以解答此题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
【题目】甲,乙,丙,丁四名跳高运动员赛前几次选拔赛成绩如表所示,根据表中的信息,如果要从中,选择一名成绩好又发挥稳定的运动员参加比赛,那么应选_____.
甲 | 乙 | 丙 | 丁 | |
平均数(cm) | 185 | 180 | 185 | 180 |
方差 | 3.6 | 3.6 | 7.9 | 8.2 |