题目内容
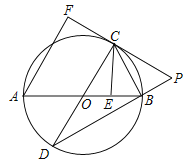
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() 是锐角,
是锐角,![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() ;若
;若![]() ,则
,则![]() 的长为( )
的长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
延长EF,DA交于G,连接DE,先证明△AFG≌△BFE,进而得到BE=AG,F是GE的中点,结合条件BF⊥GE进而得到BF是线段GE的垂直平分线,得到GD=DE,最后在Rt△AED中使用勾股定理即可求解.
解:延长EF,DA交于G,连接DE,如下图所示:
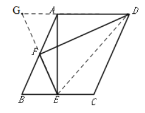
∵F是AB的中点,∴AF=BF,
∵四边形ABCD是平行四边形,
∴AB∥BC,∴∠GAB=∠EBF
且∠GFA=∠EFB,∴△AFG≌△BFE(ASA),
设![]() ,
,
由GF=EF,且∠DFE=90°知,
DF是线段GE的垂直平分线,
∴![]() ,
,
在Rt△GAE中,![]() .
.
在Rt△AED中,![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,
故选:B.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案【题目】为了解学生掌握垃圾分类知识的情况,增强学生环保意识,某学校举行了“垃圾分类人人有责”的知识测试活动,现从该校七、八年级中各随机抽取20名学生的测试成绩(满分10分,6分及6分以上为合格)进行整理、描述和分析,下面给出了部分信息.
七年级20名学生的测试成绩为:
7,8,7,9,7,6,5,9,10,9,8,5,8,7,6,7,9,7,10,6.
七、八年级抽取的学生的测试成绩的平均数、众数、中位数、8分及以上人数所占百分比如下表所示:
年级 | 平均数 | 众数 | 中位数 | 8分及以上人数所占百分比 |
七年级 | 7.5 | a | 7 | 45% |
八年级 | 7.5 | 8 | b | c |
八年级20名学生的测试成绩条形统计图如图:
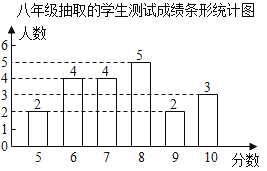
根据以上信息,解答下列问题:
(1)直接写出上述表中的a,b,c的值;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握垃圾分类知识较好?请说明理由(写出一条理由即可);
(3)该校七、八年级共1200名学生参加了此次测试活动,估计参加此次测试活动成绩合格的学生人数是多少?