题目内容
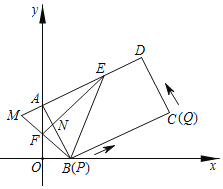
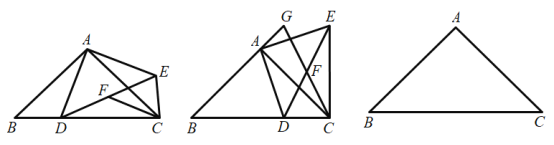
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接CE,DE.点F是DE的中点,连接CF.
,点D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接CE,DE.点F是DE的中点,连接CF.
(1)求证:![]() ;
;
(2)如图2所示,在点D运动的过程中,当![]() 时,分别延长CF,BA,相交于点G,猜想AG与BC存在的数量关系,并证明你猜想的结论;
时,分别延长CF,BA,相交于点G,猜想AG与BC存在的数量关系,并证明你猜想的结论;
(3)在点D运动的过程中,在线段AD上存在一点P,使![]() 的值最小.当
的值最小.当![]() 的值取得最小值时,AP的长为m,请直接用含m的式子表示CE的长.
的值取得最小值时,AP的长为m,请直接用含m的式子表示CE的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先证△BAD≌△CAE,可得∠ABD=∠ACE=45°,可求∠BCE=90°,由直角三角形的性质和等腰直角三角形的性质可得结论;
(2)由(1)得![]() ,
,![]() ,
,![]() ,推出
,推出![]() ,然后根据现有条件说明
,然后根据现有条件说明
在![]() 中,
中,![]() ,点A,D,C,E四点共圆,F为圆心,则
,点A,D,C,E四点共圆,F为圆心,则![]() ,在
,在![]() 中,推出
中,推出![]() ,即可得出答案;
,即可得出答案;
(3)设点P存在,由费马定理可得![]() ,设PD为
,设PD为![]() ,
,
得出![]() ,
,![]() ,得出
,得出![]() ,解出a,根据
,解出a,根据![]() 即可得出答案.
即可得出答案.
解:(1)证明如下:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴在![]() 和
和![]() 中
中 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,F为DE中点(同时
中,F为DE中点(同时![]() ),
),![]() ,
,
∴![]() ,即
,即![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
(2)由(1)得![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∵F为DE中点,
∴![]() ,
,
在四边形ADCE中,有![]() ,
,![]() ,
,
∴点A,D,C,E四点共圆,
∵F为DE中点,
∴F为圆心,则![]() ,
,
在![]() 中,
中,
∵![]() ,
,
∴F为CG中点,即![]() ,
,
∴![]() ,
,
即![]() ;
;
(3)设点P存在,由费马定理可得![]() ,
,
∴![]() ,
,
设PD为![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
![]()
![]()
又![]()
∴![]() .
.

【题目】为了解学生掌握垃圾分类知识的情况,增强学生环保意识,某学校举行了“垃圾分类人人有责”的知识测试活动,现从该校七、八年级中各随机抽取20名学生的测试成绩(满分10分,6分及6分以上为合格)进行整理、描述和分析,下面给出了部分信息.
七年级20名学生的测试成绩为:
7,8,7,9,7,6,5,9,10,9,8,5,8,7,6,7,9,7,10,6.
七、八年级抽取的学生的测试成绩的平均数、众数、中位数、8分及以上人数所占百分比如下表所示:
年级 | 平均数 | 众数 | 中位数 | 8分及以上人数所占百分比 |
七年级 | 7.5 | a | 7 | 45% |
八年级 | 7.5 | 8 | b | c |
八年级20名学生的测试成绩条形统计图如图:
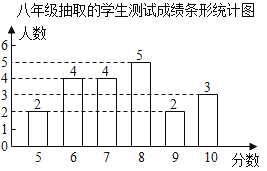
根据以上信息,解答下列问题:
(1)直接写出上述表中的a,b,c的值;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握垃圾分类知识较好?请说明理由(写出一条理由即可);
(3)该校七、八年级共1200名学生参加了此次测试活动,估计参加此次测试活动成绩合格的学生人数是多少?
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如下表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 380 | 940 |
餐椅 |
| 160 |
已知用600元购进的餐椅数量与用1300元购进的餐桌数量相同.
(1)求表中a的值;
(2)该商场计划购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.若将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售,请问怎样进货,才能获得最大利润?最大利润是多少?