题目内容
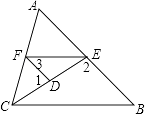
【题目】如图,CE是△ABC外角∠ACD的平分线,AF∥CD交CE于点F,FG∥AC交CD于点G,求证:四边形ACGF是菱形.
【答案】试题解析:
证明:∵AF∥CD,FG∥AC,
∴四边形ACGF是平行四边形,∠2=∠3,
∵CE平分∠ACD,
∴∠1=∠2,
∴∠1=∠3,
∴AC=AF,
∴四边形ACGF是菱形.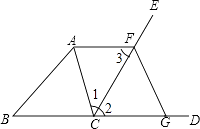
【解析】已知AF∥CD,FG∥AC,即可判定四边形ACGF是平行四边形,∠2=∠3,又因CE平分∠ACD,可得∠1=∠2,所以∠1=∠3,根据等腰三角形的判定可得AC=AF,由一组邻边相等的平行四边形是菱形可得四边形ACGF是菱形.
【考点精析】通过灵活运用平行四边形的判定,掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形即可以解答此题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目