��Ŀ����
����Ŀ������������ 
��1����ͼ1��ͼ�����ǰ�����Ϊ��8���Ρ�����˵����A+��B=��C+��D��
��2���Ķ���������ݣ��������������⣺ ��ͼ2��AP��CP�ֱ�ƽ�֡�BAD����BCD������ABC=36�㣬��ADC=16�㣬���P�Ķ�����
�⣺��AP��CP�ֱ�ƽ�֡�BAD����BCD
���1=��2����3=��4
�ɣ�1���Ľ��۵ã� ![]()
��+�ڣ���2��P+��2+��3=��1+��4+��B+��D
���P= ![]() ����B+��D��=26�㣮
����B+��D��=26�㣮
����ͼ3��ֱ��APƽ�֡�BAD����ǡ�FAD��CPƽ�֡�BCD����ǡ�BCE������ABC=36�㣬��ADC=16�㣬������P�Ķ�������˵�����ɣ�
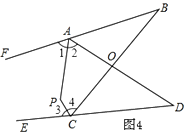
����ͼ4�У�ֱ��APƽ�֡�BAD����ǡ�FAD��CPƽ�֡�BCD����ǡ�BCE�������P���B����D�Ĺ�ϵ��ֱ��д�����ۣ�����˵�����ɣ�
����ͼ5�У�APƽ�֡�BAD��CPƽ�֡�BCD����ǡ�BCE�������P���B����D�Ĺ�ϵ��ֱ��д�����ۣ�����˵�����ɣ�
���𰸡�
��1���⣺�ߡ�A+��B+��AOB=180�㣬��C+��D+��COD=180�b��
���A+��B+��AOB=��C+��D+��COD��
�ߡ�AOB=��COD��
���A+��B=��C+��D
��2���⣺�١�P=26�b��
��APƽ�֡�BAD����ǡ�FAD��CPƽ�֡�BCD����ǡ�BCE��
���1=��2����3=��4
�ɣ�1���Ľ��۵ã���PAD+��P=��PCD+��D �٣���PAB+��P=��PCB+��B �ڣ�
�ߡ�PAB=��1����1=��2��
���PAB=��2��
���2+��P=��3+��B �ۣ�
��+�۵á�2+��P+��PAD+��P=��3+��B+��PCD+��D����2��P+180��=��B+��D+180�㣬
���P= ![]() (��B+��D ��=26�㣮
(��B+��D ��=26�㣮

����ͼ4��
��APƽ�֡�BAD����ǡ�FAD��CPƽ�֡�BCD����ǡ�BCE��
���1=��2����3=��4��
�ࣨ180�㩁2��1��+��B=��180�㩁2��4��+��D��
���ı���APCB�У���180�㩁��1��+��P+��4+��B=360�㣬
���ı���APCD�У���2+��P+��180�㩁��3��+��D=360�㣬
��2��P+��B+��D=360�㣬
���P=180�㩁 ![]() ����B+��D����
����B+��D����
����ͼ5��

��APƽ�֡�BAD��CPƽ�֡�BCD����ǡ�BCE��
���1=��2����3=��4��
�ߣ���1+��2��+��B=��180�㩁2��3��+��D��
��2+��P=��180�㩁��3��+��D��
��2��P=180��+��D+��B��
���P=90��+ ![]() ����B+��D����
����B+��D����
����������1�����������ε��ڽǺ͵���180����ʽ�������ɵ�֤����2�����ݽ�ƽ���ߵĶ���ɵá�1=��2����3=��4���ٸ��ݣ�1���Ľ����г��������ɵý⣻�ٱ�ʾ����PAD�͡�PCD���ٸ��ݣ�1���Ľ����г���ʽ���������ɵý⣻�ڸ����ı��ε��ڽǺ͵���360��ɵã�180�㩁��1��+��P+��4+��B=360�㣬��2+��P+��180�㩁��3��+��D=360�㣬Ȼ���������ɵý⣻�۸��ݣ�1���Ľ��ۡ�B+��BAD=��D+��BCD����PAD+��P=��D+��PCD��Ȼ���������ɵý⣮
�����㾫�����������⣬������Ҫ�˽������ε��ڽǺ����(�����ε������ڽ��У�ֻ������һ���ڽ���ֱ�ǻ�۽ǣ�ֱ�������ε�������ǻ��ࣻ�����ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽ�)����Ҫ���������ε����(������һ������һ�ߵ��ӳ�����ɵĽǣ��������ε���ǣ������ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽ�)�����֪ʶ���Ǵ���Ĺؼ���

����Ŀ���ס��ҡ��������ĸ�С���ͬѧ�ֱ�μ��˰�����֯���л���ʫ��֪ʶ����������ͬ�����¸�С��ijɼ����±���ʾ����Ҫ����ѡ��һ��С��μ��꼶�ı�������ôӦѡ�� ��
���� | ���� | ���� | ���� | |
ƽ���� | 85 | 90 | 88 | 90 |
���� | 3.5 | 3.5 | 4 | 4.2 |
A. ����B. ����C. ����D. ����

