题目内容
【题目】完成证明,说明理由. 已知:如图,点D在BC边上,DE、AB交于点F,AC∥DE,∠1=∠2,∠3=∠4.
求证:AE∥BC.
证明:∵AC∥DE(已知),
∴∠4=()
∵∠3=∠4(已知),
∴∠3=()
∵∠1=∠2(已知),
∴∠1+∠FAD=∠2+∠FAD()
即∠FAC=∠EAD,
∴∠3= .
∴AE∥BC()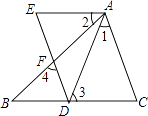
【答案】∠FAC;两直线平行,同位角相等;∠FAC;等量代换;等式的性质;∠EAD;内错角相等,两直线平行
【解析】解:∵AC∥DE(已知), ∴∠4=∠FAC(两直线平行,同位角相等)
∵∠3=∠4(已知),
∴∠3=∠FAC(等量代换)
∵∠1=∠2(已知),
∴∠1+∠FAD=∠2+∠FAD(等式的性质)
即∠FAC=∠EAD,
∴∠3=∠EAD.
∴AE∥BC(内错角相等,两直线平行 ).
所以答案是:∠FAC;两直线平行,同位角相等;∠FAC;等量代换;等式的性质;∠EAD;内错角相等,两直线平行.
【考点精析】本题主要考查了平行线的判定的相关知识点,需要掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行才能正确解答此题.

练习册系列答案
相关题目
【题目】迎接学校“元旦”文艺汇演,八年级某班的全体同学捐款购买了表演道具,经过充分的排练准备,最终获得了一等奖.班长对全体同学的捐款情况绘制成下表:
捐款金额 | 5元 | 10元 | 15元 | 20元 |
捐款人数 | 10人 | 15人 |
| 5人 |
由于填表时不小心把墨水滴在了统计表上,致使表中数据不完整,但知道捐款金额为10元的人数为全班人数的30%,结合上表回答下列问题:
(1)该班共有名同学;
(2)该班同学捐款金额的众数是元,中位数是元.
(3)如果把该班同学的捐款情况绘制成扇形统计图,则捐款金额为20元的人数所对的扇形圆心角为度.