Question

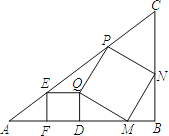
【题目】如图，AB∥CD，连结AD，点E是AD的中点，连结BE并延长交CD于F点．

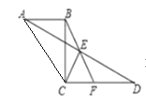
（1）请说明△ABE≌△DFE的理由；

（2）连结CE，AC,若CB⊥CD，AC=CD,∠D=30°，CD=2，求BF的长．

Answer 1

【答案】（1）见解析；（2）2

【解析】

（1）由条件可得∠BAE=∠EDF，AE=ED，∠AEB=∠FED，则根据ASA可证明结论；
（2）由等腰三角形的性质可得CE⊥AD，求出CE=1，证明BF=2CE，则BF可求出．

证明：∵AB∥CD ∴∠BAE=∠EDF

∵点E是AD的中点 ∴AE=ED

又∵∠AEB=∠FED

∴△ABE≌△DFE（ASA）

（2）解：∵AC=CD 且E为AD中点 ∴CE⊥AD

∵∠D=30°且CD=2 ∴CE=1

又∵CB⊥CD且BE=EF ∴BF=2CE

∴BF=2