题目内容
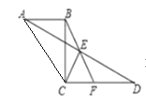
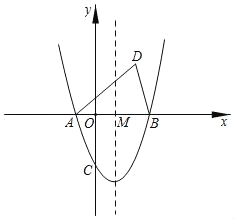
【题目】如图,抛物线y=x2+bx+c与x轴交于点A(﹣1,0)、B两点,与y轴交于点C(0,﹣3).
(1)求抛物线的函数解析式;
(2)已知点P(m,n)在抛物线上,当﹣2≤m<3时,直接写n的取值范围;
(3)抛物线的对称轴与x轴交于点M,点D与点C关于点M对称,试问在该抛物线上是否存在点P,使△ABP与△ABD全等?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.
【答案】(1)y=x2﹣2x﹣3;(2)﹣4≤n≤5;(3)P的坐标为(0,﹣3)或(2,﹣3).
【解析】
(1)将A,C两点的坐标代入解析式可得抛物线的解析式;
(2)根据二次函数的性质可求n的取值范围;
(3)在x轴上方的P不存在,点P只可能在x轴的下方,按照题意,分别求解即可.
解:(1)将点C坐标代入函数表达式得:y=x2+bx﹣3,
将点A的坐标代入上式并解得:b=﹣2,
故抛物线的表达式为:y=x2﹣2x﹣3;
(2)令y=x2﹣2x﹣3=0,则x=3或﹣1,即点B(3,0),
函数的对称轴为x=1,
m=﹣2时,n=4+4﹣3=5,
m<3,函数的最小值为顶点纵坐标的值:﹣4,
故﹣4≤n≤5;
(3)点D与点C(0,﹣3)关于点M对称,则点D(2,3),
在x轴上方的P不存在,点P只可能在x轴的下方,
如下图当点P在对称轴右侧时,点P为点D关于x轴的对称点,此时△ABP与△ABD全等,
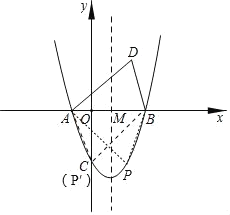
即点P(2,﹣3);
同理点C(P′)也满足△ABP′与△ABD全等,
即点P′(0,﹣3);
故点P的坐标为(0,﹣3)或(2,﹣3).

 步步高达标卷系列答案
步步高达标卷系列答案【题目】某保健品厂每天生产A,B两种品牌的保健品共600瓶,A,B两种产品每瓶的成本和售价如下表,设每天生产A产品x瓶,生产这两种产品每天共获利y元.
A | B | |
成本(元)/瓶 | 50 | 35 |
售价(元)/瓶 | 70 | 50 |
(1)请求出y关于x的函数关系;
(2)该厂每天生产的A,B两种产品被某经销商全部订购,厂家对B产品不变,对A产品进行让利,每瓶利润降低![]() 元,厂家如何生产可使每天获利最大?最大利润是多少?
元,厂家如何生产可使每天获利最大?最大利润是多少?