题目内容
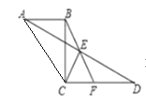
【题目】如图1,点E为正方形ABCD的边CD上一点,DF⊥AE于点F,交AC于点M,交BC于点G,在CD上取一点G′,使CG′=CG.连接MG′.

(1)求证:∠AED=∠CG′M;
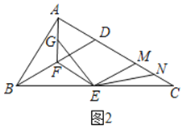
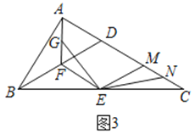
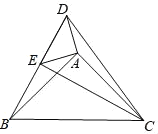
(2)如图2,连接BD交AE于点N,连接MN,MG′交AE于H.
①试判断MN与CD的位置关系,并说明理由;
②若AB=12,DG′=G′E,求AH的长.
【答案】(1)见解析;(2)①MN∥CD,见解析;②AH=3![]() .
.
【解析】
(1)如图1,根据同角的余角相等可得:∠AED=∠DGC,证明△GCM≌△G'CM,即可得出∠AED=∠CG'M;
(2)①根据同位角相等,两直线平行,由∠ONM=45°,∠ODC=45°,则∠ONM=∠ODC,则MN∥CD;
②如图2,先证明△ADE≌△DCG,则DE=CG=CG',可知E、G'是DC的三等分点,则CG=2BG=8,根据勾股定理得:AE=4![]() =4,由平行线分线段成比例定理的比例式,计算AN和EN的长,由勾股定理可得ON的长,由MN∥EG',则△MNH∽△G'EH,列比例式可得结论.
=4,由平行线分线段成比例定理的比例式,计算AN和EN的长,由勾股定理可得ON的长,由MN∥EG',则△MNH∽△G'EH,列比例式可得结论.
(1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠ADC=∠DCG=90°,
∴∠DGC+∠CDG=90°,
∵AE⊥DF,
∴∠DFE=90°,
∴∠AED+∠CDG=90°,
∴∠AED=∠DGC,
∵CG=CG',∠MCG=∠MCG',CM=CM,
∴△GCM≌△G'CM,
∴∠DGC=∠CG'M,
∴∠AED=∠CG'M;
(2)解:①MN∥CD,理由如下:
∵∠AOD=∠NFD=90°,∠ANO=∠DNF,
∴∠OAN=∠ODM,
∵AO=OD,∠AON=∠DOM=90°,
∴△AON≌△DOM,
∴ON=OM,
∴△NOM是等腰直角三角形,
∴∠ONM=45°,
∵∠ODC=45°,
∴∠ONM=∠ODC,
∴MN∥CD;
②在△ADE和△DCG中,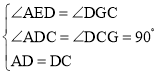 ,
,
∴△ADE≌△DCG(AAS),
∴DE=CG,
∵CG=CG',
∴CG'=CG=DE,
∴DG'=CE=EG'=![]() CD=
CD=![]() AB=4,
AB=4,
∴CG=2BG=8,
由勾股定理得:AE=![]() =4
=4![]() ,
,
∵AB∥DE,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴AN=![]() ×4
×4![]() =
=![]() ,EN=
,EN=![]() ×4
×4![]() =
=![]() ,
,
∵AO=![]() =6
=6![]() ,
,
∴ON=![]() =
=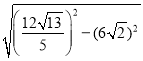 =
=![]() ,
,
∵△MON是等腰直角三角形,
∴MN=![]() ON=
ON=![]() ,
,
∵MN∥EG',
∴△MNH∽△G'EH,
∴![]() =
=![]() =
=![]() ,
,
∴NH=![]() ×
×![]() =
=![]() ,EH=
,EH=![]() ×
×![]() =
=![]() ,
,
∴AH=AE﹣EH=4![]() ﹣
﹣![]() =3
=3![]() .
.

 阅读快车系列答案
阅读快车系列答案