Question

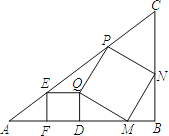
【题目】如图，Rt△ABC中，∠B=90°，正方形EFDQ、正方形MNPQ公共顶点记为点Q，其余的各个顶点都在Rt△ABC的边上，若AC=5，BC=3，则EP=____________．

Answer 1

【答案】．

【解析】

过P作BC垂线，垂足为G，可证△QDM≌△MBN≌△NGP，△AEF∽△PGC∽△ABC设EF=3a，CG=3b，则AE=5a，AF=4a，PC=5b，PG=4b，可列二元一次方程组：3a+7b=3，10a+4b=4，求出a、b的值，代入EP=5-5a-5b求出即可．

在Rt△ABC中，∠B=90°，AC=5，BC=3，由勾股定理得：AB=4，

过P作PG⊥BC于G，

∵四边形EFDQ和四边形QMNP是正方形，

∴∠CGP=∠QMN=∠QDF=∠B=90°，PN=MN=MQ，

∴∠GPN+∠GNP=90°，∠GNP+∠BNM=90°，

∴∠GPN=∠BNM，

同理∠BNM=∠QMD，

在△GPN、△BNM、△DMQ中，

∠PGN=∠B=∠QDM=90°，∠GPN=∠BNM=∠DMQ，PN=MN=QM，

∴△QDM≌△MBN≌△NGP，

∴PG=BN=DM，GN=BM=DQ，

∵∠PGC=∠B=90°，

∴△CGP∽△CBA，

∴，

∴

同理，，

设EF=3a，CG=3b，则AE=5a，AF=4a，PC=5b，PG=4b=BN=DM，GN=BM=DQ=EF=3a，

可列一元二次方程组：

解得：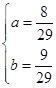

EP=5-5a-5b=．