题目内容
【题目】如图,图①是一个长为2m,宽为2n的长方形.沿图中虚线把它分割成四块完全相同的小长方形,然后按图②的形状拼成一个正方形.
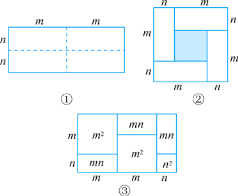
(1)求图②中阴影部分的面积.
(2)观察图②,发现三个代数式(m+n)2,(m-n)2,mn之间的等量关系是 .
(3)若x+y=-6,xy=2.75,求x-y的值.
(4)观察图③,你能得到怎样的代数恒等式?
(5)试画出一个几何图形,使它的面积能表示代数恒等式(m+n)(m+3n)=m2+4mn+3n2.
【答案】(1)(m-n)2或(m+n)2-4mn;(2) (m-n)=(m+n)-4mn;(3)±5;(4)(m+n)(2m+n)=2m2+3mn+n2;(5)见解析.
【解析】
(1)可直接用正方形的面积公式得到;(2)熟练掌握完全平方公式,并掌握和与差的区别;(3)此题可参照第二题;(4)可利用各部分面积和=长方形面积列出恒等式;(5)可参照第四题画图.
(1)(m-n)2或(m+n)2-4mn.
(2)(m-n)2=(m+n)2-4mn;
(3)(x-y)2=(x+y)2-4xy
=(-6)2-4×2.75
=36-11
=25.
∴x-y=±![]() =±5.
=±5.
(4)(m+n)(2m+n)=2m2+3mn+n2.
(5)如解图所示(答案不唯一).


练习册系列答案
相关题目