题目内容
【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
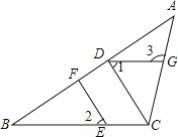
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,CD平分∠ACB,且∠3=120°,求∠ACB与∠1的度数.
【答案】(1)详见解析;(2)∠ACB=120°,∠1=60°
【解析】
(1)根据垂直于同一直线的两直线平行判定;
(2)根据平行线的性质和已知求出∠1=∠2=∠DCB,推出DG∥BC,根据平行线的性质得出∠ACB的度数即可;再由∠ACB的度数和已知得∠DCG的度数,利用三角形的外角的性质即可求出∠1的度数.
解:(1)CD∥EF,
理由是:∵CD⊥AB,EF⊥AB,
∴CD∥EF;
(2)∵CD∥EF,
∴∠2=∠DCB,
∵∠1=∠2,
∴∠1=∠DCB,
∴DG∥BC,
∴∠ACB=∠3,
∵∠3=120°,
∴∠ACB=120°.
∵CD平分∠ACB,
∴∠DCG=![]() ∠ACB=60°,
∠ACB=60°,
∵∠3=∠1+∠DCG,
∴∠1=120°-60°=60°.
∴∠ACB=120°,∠1=60°.

练习册系列答案
相关题目