题目内容
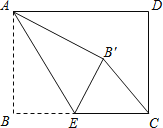
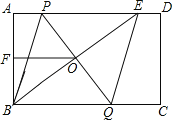
【题目】如图,在矩形ABCD中,E是AD边上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、QE
(1)求证:四边形BPEQ是菱形:
(2)若AB=6,F是AB中点,OF=4,求菱形BPEQ的面积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)先根据线段垂直平分线的性质证明PB=PE,由ASA证明△BOQ≌△EOP,得出PE=QB,证出四边形BPEQ是平行四边形,再根据菱形的判定即可得出结论;
(2)先证明OF为△BAE的中位线,然后依据三角形的中位线定理得出AE∥OF且OF=![]() AE.求得OB的长,则可得到BE的长,设菱形的边长为x,则AP=8﹣x,在Rt△APB中依据勾股定理可列出关于x的方程,然后依据菱形的面积公式进行计算即可.
AE.求得OB的长,则可得到BE的长,设菱形的边长为x,则AP=8﹣x,在Rt△APB中依据勾股定理可列出关于x的方程,然后依据菱形的面积公式进行计算即可.
(1)证明:∵PQ垂直平分BE,
∴PB=PE,OB=OE,
∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠PEO=∠QBO,
在△BOQ与△EOP中,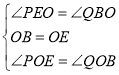 ,
,
∴△BOQ≌△EOP(ASA),
∴PE=QB,
又∵AD∥BC,
∴四边形BPEQ是平行四边形,
又∵QB=QE,
∴四边形BPEQ是菱形;
(2)解:∵AB=6,F是AB的中点,
∴BF=3.
∵四边形BPEQ是菱形,
∴OB=OE.
又∵F是AB的中点,
∴OF是△BAE的中位线,
∴AE∥OF且OF=![]() AE.
AE.
∴∠BFO=∠A=90°.
在Rt△FOB中,OB=![]() =5,
=5,
∴BE=10.
设菱形的边长为x,则AP=8﹣x.
在Rt△APB中,BP2=AB2+AP2,
即x2=62+(8﹣x)2,
解得:x=![]() ,
,
∴BQ=![]() ,
,
∴菱形BPEQ的面积=BQ×AB=![]() ×6=
×6=![]() .
.

练习册系列答案
相关题目