Question

【题目】求证：三角形的中位线平行于三角形的第三边，并且等于第三边的一半．解答要求如下：

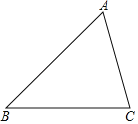
（1）对于图中△ABC，用尺规作出一条中位线DE；（不必写作法，但应保留作图痕迹）

（2）根据（1）中作出的中位线，写出已知，求证和证明过程．

Answer 1

【答案】（1）见解析；（2）已知△ABC中，D、E分别是AB、AC的中点，求证：DE=BC，见解析.

【解析】

（1）分别作AB、AC的中垂线，交AB、AC于点D、E，连接DE．线段DE即为所求．

（2）利用相似三角形的性质即可证明．

解：（1）分别作AB、AC的中垂线，交AB、AC于点D、E，连接DE．

线段DE即为所求．

（2）已知△ABC中，D、E分别是AB、AC的中点，

求证：DE=BC

证明：∵D、E分别是AB、AC的中点，

∴＝＝，

又∠A＝∠A，

∴△ADE∽△ABC，

∴∠ADE＝∠B，

∴DE∥BC，

∴＝＝，

∴DE＝BC．