题目内容
【题目】如图,将长BC=8cm,宽AB=4cm的矩形纸片ABCD折叠,使点C与点A重合,则折痕EF的长为( )

![]()

A. 4cmB. ![]() cmC.
cmC. ![]() cmD.
cmD. ![]() cm
cm
【答案】C
【解析】
连结AC交EF于O, 设EC=EA=(x)cm,则BE=(8-x)cm,根据勾股定理求出x.由两直线平行和折叠得出∠AFE=∠FEA,从而得出AE=AF=EC,推出四边形AECF为菱形;根据菱形的性质和勾股定理即可得出.
如图所示,补全矩形ABCD,连结AC交EF于O.
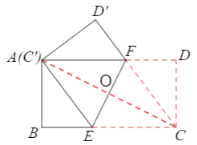
设EC=EA=(x)cm,则BE=(8-x)cm.
在Rt△ABE中,有AE2=AB2+BE2,
即x2=(8-x)2+42,解得x=5.
∵AD∥BC,
∴∠FEC=∠AFE,
而由折叠可知,∠FEC=∠FEA,AE=EC,
∴∠AFE=∠FEA.
∴AE=AF=EC.
而AF∥EC,
∴四边形AECF为菱形,从而有AC⊥EF.
在Rt△ABC中,AC=![]() =4
=4![]() ,则OC=
,则OC=![]() AC=2
AC=2![]() .
.
在Rt△COE中,OE=![]() =
=![]() .
.
∴EF=2OE=2![]() .
.
故选:C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目