题目内容
【题目】如图,已知,在△ABC中,CA=CB,∠ACB=90°,E,F分别是CA,CB边的三等分点,将△ECF绕点C逆时针旋转α角(0°<α<90°),得到△MCN,连接AM,BN. 
(1)求证:AM=BN;
(2)当MA∥CN时,试求旋转角α的余弦值.
【答案】
(1)解:∵CA=CB,∠ACB=90°,E,F分别是CA,CB边的三等分点,
∴CE=CF,
根据旋转的性质,CM=CE=CN=CF,∠ACM=∠BCN=α,
在△AMC和△BNC中,
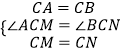 ,
,
∴△AMC≌△BNC,
∴AM=BN
(2)解:∵MA∥CN,
∴∠ACN=∠CAM,
∵∠ACN+∠ACM=90°,
∴∠CAM+∠ACM=90°,
∴∠AMC=90°,
∴cosα= ![]() .
.
【解析】(1)由CA=CB,E,F分别是CA,CB边的三等分点,得CE=CF,根据旋转的性质,CM=CE=CN=CF,∠ACM=∠BCN=α,证明△AMC≌△BNC即可;(2)当MA∥CN时,∠ACN=∠CAM,由∠ACN+∠ACM=90°,得到∠CAM+∠ACM=90°,所以cosα= ![]() =
= ![]() .
.
【考点精析】根据题目的已知条件,利用旋转的性质的相关知识可以得到问题的答案,需要掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


