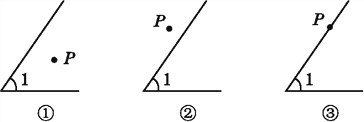
��Ŀ����
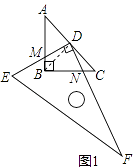
����Ŀ����ͼ1����֪��ABC�У�AB=BC=1����ABC=90�㣬��һ�麬30��ǵ����ǰ�DEF��ֱ�Ƕ���D����AC���е��ϣ�ֱ�����ǰ�Ķ�ֱ�DZ�ΪDE����ֱ�DZ�ΪDF������ֱ�����ǰ�DEF��D�㰴��ʱ�뷽����ת�� 
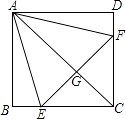
��1����ͼ1�У�DE��AB��M��DF��BC��N����֤��DM=DN��������һ�����У�ֱ�����ǰ�DEF���ABC���ص�����Ϊ�ı���DMBN����˵���ı���DMBN������Ƿ����仯���������仯����˵������α仯�ģ����������仯������������
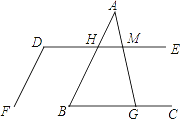
��2��������ת����ͼ2��λ�ã��ӳ�AB��DE��M���ӳ�BC��DF��N��DM=DN�Ƿ���Ȼ�������������������֤����������������˵�����ɣ�
��3��������ת����ͼ3��λ�ã��ӳ�FD��BC��N���ӳ�ED��AB��M��DM=DN�Ƿ���Ȼ�������������������д�����ۣ�����֤����
���𰸡�
��1���⣺����ͼ1������DB����Rt��ABC�У�AB=BC��AD=DC��
��DB=DC=AD����BDC=90�㣬
���ABD=��C=45�㣬
�ߡ�MDB+��BDN=��CDN+��BDN=90�㣬
���MDB=��NDC��
���BMD�ա�CND��ASA����
��DM=DN��
���ı���DMBN������������仯��
�ɢ�֪��BMD�ա�CND��
��S��BMD=S��CND��
��S�ı���DMBN=S��DBN+S��DMB=S��DBN+S��DNC=S��DBC= ![]() S��ABC=
S��ABC= ![]() ��
�� ![]() =
= ![]() ��
��
��2���⣺DM=DN��Ȼ������
֤������ͼ2������DB����Rt��ABC�У�AB=BC��AD=DC��
��DB=DC����BDC=90�㣬
���DCB=��DBC=45�㣬
���DBM=��DCN=135�㣬
�ߡ�NDC+��CDM=��BDM+��CDM=90�㣬
���CDN=��BDM��
���ڡ�BMD�͡�CND�У�  ��
��
���BMD�ա�CND��ASA����
��DM=DN��

��3���⣺DM=DN��
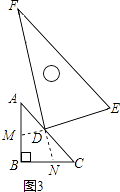
����������1������BD��֤����DMB�ա�DNC��������֪��ȫ�������Ѿ߱���������֤����MDB=��NDC����ASA֤��ȫ�ȣ��ı���DMBN������������仯����Ϊ�������ʼ�յ��ڡ�ABC�����һ�룻��2��������ͬ�����ã�1���е�֤����������֤����DMB�ա�DNC����3��������Ȼ����������ͬ��1����
�����㾫�������յ���ֱ�������κ���ת�������ǽ����ĸ�������Ҫ֪������ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣻����ת���Ӧ���߶γ��̲��䣬��ת�Ƕȴ�С���䣻����ת���Ӧ�ĵ㵽��ת����ת���ĵľ��벻�䣻����ת�������ͼ�β��䣬ֻ��λ�ñ��ˣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�