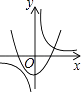题目内容
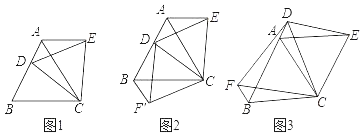
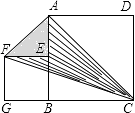
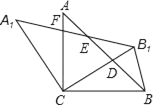
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设CB1交AB于D,A1B1分别交AB,AC于E,F
(1)求证:△CBD≌△CA1F;
(2)试用含α的代数式表示∠B1BD;
(3)当α等于多少度时,△BB1D是等腰三角形.
【答案】(1)证明见解析;(2)∠B1BD=45°﹣![]() ;(3)当△BB1D为等腰三角形时,α=30°.
;(3)当△BB1D为等腰三角形时,α=30°.
【解析】
(1)根据已知条件,利用旋转的性质及全等三角形的判定方法,来判定三角形全等;
(2)利用等腰直角三角形的性质得到∠CBA=45°.然后由旋转的性质推知BC=B1C,则∠CB1B=∠CBB1,所以根据三角形内角和定理进行解答即可;
(3)当△BBD是等腰三角形时,要分别讨论B1B=B1D、BB1=BD、B1D=DB三种情况,第一,三种情况不成立,只有第二种情况成立,求得α=30°.
(1)证明:∵AC=BC,
∴∠A=∠ABC.
∵△ABC绕点C逆时针旋转角α(0°<α<90°)得到△A1B1C,
∴∠A1=∠A,A1C=AC,∠ACA1=∠BCB1=α.
∴∠A1=∠CBD,A1C=BC.
在△CBD与△CA1F中,
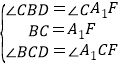 ,
,
∴△CBD≌△CA1F(ASA).
(2)∵在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°.
又由旋转的性质得到BC=B1C,则∠CB1B=∠CBB1,
∴∠CB1B=∠CBB1=![]() =90°﹣
=90°﹣![]() .
.
∴∠B1BD=∠CBB1﹣∠CBA=90°﹣![]() ﹣45°=45°﹣
﹣45°=45°﹣![]() ;
;
(3)在△CBB1中,∵CB=CB1
∴∠CBB1=∠CB1B=![]() (180°﹣α).
(180°﹣α).
又∵△ABC是等腰直角三角形,
∴∠ABC=45°.
①若B1B=B1D,则∠B1DB=∠B1BD,
∵∠B1DB=45°+α,∠B1BD=∠CBB1﹣45°=![]() (180°﹣α)﹣45°=45°﹣
(180°﹣α)﹣45°=45°﹣![]() ,
,
∴45°+α=45°﹣![]() ,
,
∴α=0°(舍去);
②∵∠BB1C=∠B1BC>∠B1BD,
∴BD>B1D,即BD≠B1D;
③若BB1=BD,则∠BDB1=∠BB1D,即45°+α=![]() (180°﹣α),α=30°
(180°﹣α),α=30°
由①②③可知,当△BB1D为等腰三角形时,α=30°.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案【题目】某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0,每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比,经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12),符合关系式x=2n2﹣2kn+9(k+3)(k为常数),且得到了表中的数据.
月份n(月) | 1 | 2 |
成本y(万元/件) | 11 | 12 |
需求量x(件/月) | 120 | 100 |
(1)求y与x满足的关系式,请说明一件产品的利润能否是12万元;
(2)求k,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第m个月和第(m+1)个月的利润相差最大,求m.