题目内容
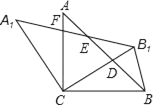
【题目】如图，正方形ABCD的边长为2，点E在AB边上．四边形EFGB也为正方形，则△AFC的面积S为 ．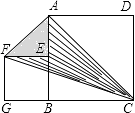 
【答案】2
【解析】解：∵正方形ABCD和正方形EFGB，
∴AB=BC=CD=AD，EF=FG=GB=BE，
∵正方形ABCD的边长为2，
∴S△AFC=S梯形ABGF+S△ABC﹣S△CGF
= 
×（FG+AB）×BG+ ×AB×BC﹣ ×FG×CG
= ×（FG+AB）×BG+ ×AB×BC﹣ ×FG×（BC+BG）
= ×FG2+FG+2﹣FG﹣ ×FG2
=2．
解法二：连接FB
∵∠CAB=∠ABF=45°
∴FB∥AC
又∵△ABC和△AFC有同底AC且等高
∴S△AFC=S△ABC= ×2×2=2
所以答案是：2．
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识，掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质，以及对三角形的面积的理解，了解三角形的面积=1/2×底×高．
练习册系列答案
优加精卷系列答案
相关题目
【题目】新房装修后，某居民购买家用品的清单如下表，因污水导致部分信息无法识别，根据下表解决问题：
家居用品名称 | 单价（元） | 数量（个） | 金额（元） |
垃圾桶 | 15 | ||
鞋架 | 40 | ||
字画 | a | 2 | 90 |
合计 | 5 | 185 | |
（1）居民购买垃圾桶，鞋架各几个？
（2）若居民再次购买字画和垃圾桶两种家居用品共花费150元，则有哪几种不同的购买方案？
